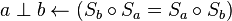Drehungen als Geradenspiegelungen (2011/12)

Beziehung zwischen "senkrecht" und Kommutativität

Satz

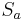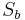Es seien $S_a$ und $S_b$ zwei Geradenspiegelungen, deren Spiegelgeraden $a$ und $b$ nicht identisch sind.

Es gilt die folgende Äquivalenz:

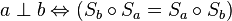$a \perp b \Leftrightarrow (S_b \circ S_a = S_a \circ S_b)$--Sternchen 11:27, 1. Dez. 2011 (CET)

Beweisteil I: 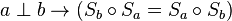$a \perp b \rightarrow (S_b \circ S_a = S_a \circ S_b)$

Um diesen Beweis führen zu können, müssen wir uns auf den Reduktionssatz rückbesinnen. Dieser zeigte uns an, dass jede Drehung die NAF zweier Geradenspiegelungen ist. Ferner konnten wir zeigen, dass es unendlich viele Geradenpaare gibt, die die Bewegung ausführen.

Seien A, B, C drei nichtkollineare Punkte und 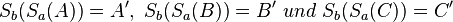$S_b(S_a(A)) = A', \ S_b(S_a(B)) = B' \ und \ S_b(S_a(C)) = C'$

Bleibt zu zeigen, dass 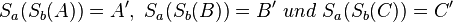$S_a(S_b(A)) = A', \ S_a(S_b(B)) = B' \ und \ S_a(S_b(C)) = C'$.

Weil ich unendlich viele Geradenpaare habe, für die gilt, dass 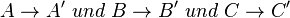$A \rightarrow A' \ und \ B \rightarrow B' \ und \ C \rightarrow C'$ kann ich mit ein weiteres Paar aussuchen. Ein weiterer Aspekt muss jedoch berücksichtigt werden: Der Schnittwinkel der beiden Geraden muss immer identisch sein. Wenn nun a' so gelegt wird, dass a' = b ist und b' so gelegt wird, dass b' = a ist, dann sind wir fertig, da nun gilt, dass 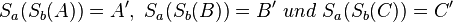$S_a(S_b(A)) = A', \ S_a(S_b(B)) = B' \ und \ S_a(S_b(C)) = C'$. --Flo60 23:23, 4. Dez. 2011 (CET)