Dreieckskongruenz SoSe 2017
StreckenkongruenzWir erinnern uns an die Diskussion zu Anfang des Semesters.
Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz. Definition VII.1: (Streckenkongruenz)
Satz VII.1:
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen. WinkelkongruenzAnalog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben. Definition VII.2 : (Winkelkongruenz)
Satz VII.2:
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen. DreieckskongruenzIn der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen. Definition VII.3: (Dreieckskongruenz)
Satz VII.3:
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
In den Schullehrbüchern findet man häufig Konstruktionsaufgaben wie: Das Kongruenzaxiom SWSAxiom V: (Kongruenzaxiom SWS)
Der Kongruenzsatz WSWSatz VII.4: (Kongruenzsatz WSW)
Beweis von Satz VII.4Als Folge von TafelnDie BeweisideeTesten Sie Ihr Verständnis: Beschreiben Sie hier mit drei ganz einfachen Sätzen, auf welcher Idee der Beweis beruht.
|
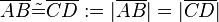
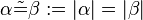
 und
und  die folgenden 6 Kongruenzen
die folgenden 6 Kongruenzen
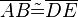
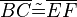
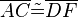
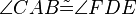
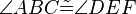
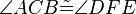
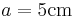 ,
, 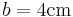 ,
, 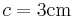 .
. 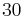 Schüler konstruieren aufgrund dieser Aufgabenstellung
Schüler konstruieren aufgrund dieser Aufgabenstellung 
