Dreieckskongruenz WS 12 13
Die beiden grundlegenden Ideen der KongruenzBewegungsgeometrienaive DeckungsgleichheitZwei Figuren sind deckungsgleich, wenn sie ausgeschnitten so aueinander platziert werden könne, dass nichts übersteht bzw. die beiden Figuren genau aufeinander passen. Bewegungen: abstandserhaltende Abbildungen der Ebene auf sichDefinition (Bewegung oder Kongruenzabbildung) Zueinander kongruente FigurenDefinition (Figur) Definition (Relation der Kongreunz auf der Menge aller Figuren) Euklid lässt grüßen: DreieckskongruenzVideos zur Idee der KongruenzStreckenkongruenzWir erinnern uns an die Diskussion zu Anfang des Semesters.
Momentan jedoch eigentlich noch nicht. Uns fehlt eine Definition des Begriffs der Streckenkongruenz. Definition VII.1: (Streckenkongruenz)
WinkelkongruenzAnalog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben. Definition VII.2 : (Winkelkongruenz)
DreieckskongruenzIn der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen. Definition VII.3: (Dreieckskongruenz)
Überprüfen Sie Ihr Verständnis: In den Schullehrbüchern findet man häufig Konstruktionsaufgaben wie: Das Kongruenzaxiom SWSAxiom V: (Kongruenzaxiom SWS)
Der Kongruenzsatz WSWSatz VII.4: (Kongruenzsatz WSW)
Beweis von Satz VII.4Als Folge von TafelnDie BeweisideeTesten Sie Ihr Verständnis: Beschreiben Sie hier mit drei ganz einfachen Sätzen, auf welcher Idee der Beweis beruht.
Der Kongruenzsatz SSSHier dürfen Sie sich austoben. Für den Beweis des Kongruenzsatzes SSS werden Sie sinnvollerweise den Basiswinkelsatz benötigen. Weil dieser jedoch von so zentraler Bedeutung ist, haben wir ihm einen eigenen Unterpunkt auf der Hauptseite spendiert. Sie dürfen ihn also hier vorab als wahr voraussetzen. Hilfe finden Sie in Über die Grundlagen der Geometrie bzw. Höhere Geometrie I von Nikolaĭ Vladimirovich Efimov (Никола́й Влади́мирович Ефи́мов) im Lesesaal. Der Kongruenzsatz SsWHier dürfen Sie sich austoben. Hinweis: Alle Kongruenzsätze dürfen ab sofort in Beweisen verwendet werden. |
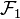 und
und 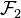 sind kongruent zueinander (in Zeichen
sind kongruent zueinander (in Zeichen 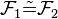 ), wenn es eine Bewegung
), wenn es eine Bewegung  mit
mit 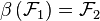 gibt.
gibt.
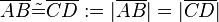
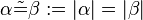
 und
und  die folgenden 6 Kongruenzen
die folgenden 6 Kongruenzen
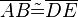
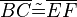
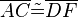
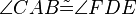
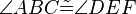
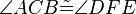
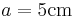 ,
, 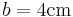 ,
, 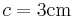 .
. 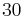 Schüler konstruieren aufgrund dieser Aufgabenstellung
Schüler konstruieren aufgrund dieser Aufgabenstellung 
