Eigenschaften und Rechenregeln bei beliebigen Vektorräumen
Aus Geometrie-Wiki
i) Für alle Vektoren 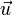 ist
ist 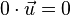
ii) Der Nullvektor 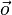 ist eindeutig bestimmt.
ist eindeutig bestimmt.
iii) Für alle 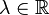 ist
ist 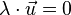 .
.
iv) Für jeden Vektor 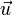 ist der Gegenvektort
ist der Gegenvektort 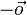 eindeutig bestimmt.
eindeutig bestimmt.
v) Für alle Vektoren 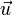 und alle
und alle 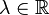 ist
ist 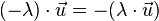 .
.
vi) Für alle Vektoren 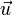 und alle
und alle 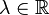 ist
ist 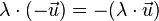 .
.
vii) Für alle Vektoren 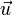 und alle
und alle 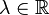 gilt: Aus
gilt: Aus 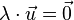 folgt
folgt 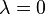 oder
oder 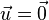
Beweis: Siehe Filler Elementare Lineare Algebra S.111

