Beispiel 1
Experimentieren Sie: Wann ist die Menge Fehler beim Parsen(Syntaxfehler): \left{\vec{a}, \vec{b}\right}
ein Erzeugendensystem für den 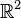 bzw. für die Menge aller Pfeilklassen der Ebene. (Strg+f frischt den Bildschirm auf) bzw. für die Menge aller Pfeilklassen der Ebene. (Strg+f frischt den Bildschirm auf)
Beispiel 2
Erzeugendensystem, Basis und Hülle
Def.(lineare Hülle)
Lineare Hülle der Vektoren 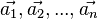 ist die Menge der Linearkombinationen von ist die Menge der Linearkombinationen von 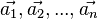
Das bedeutet, die lineare Hülle der Vektoren 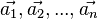 enthält alle Vektoren, die man mithilfe der Vektoren enthält alle Vektoren, die man mithilfe der Vektoren 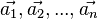 darstellen kann. darstellen kann.
Def.(Erzeugendensystem)
Eine Menge von Vektoren 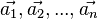 ist ein Erzeugendensystem enes Vektorraumes V, wenn V eine Teilmenge der linearen Hülle von ist ein Erzeugendensystem enes Vektorraumes V, wenn V eine Teilmenge der linearen Hülle von 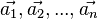 ist. ist.
Das heißt, wenn man mit den Vektoren 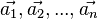 alle Vektoren des Vektorraumes V darstellen kann ist die Menge der Vektoren alle Vektoren des Vektorraumes V darstellen kann ist die Menge der Vektoren 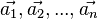 ein Erzeugendensystem von V. ein Erzeugendensystem von V.
Die Menge der Vektoren 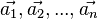 kann linear abhängig sein. kann linear abhängig sein.
Def.(Basis)
B ist eine Basis, wenn B ein Erzeugendensystem ist und linear unabhängig.
Daraus folgt, dass eine Basis eines Vektorraumes V ein minimales Erzeugendensystem ist.
|