Ganze Zahlen mit der Multiplikation
Aus Geometrie-Wiki
Im Grunde ist die Überprüfung, ob es sich bei ![[\Z,\sdot]](/images/math/a/0/3/a037444a418c44fefd7d03f7b97e2d91.png) um eine Gruppe handelt, mit dem Verweis auf die Natürliche Zahlen mit Multiplikation schon beinahe trivial.
um eine Gruppe handelt, mit dem Verweis auf die Natürliche Zahlen mit Multiplikation schon beinahe trivial.
Dennoch hier ein analog geführtes (Gegen)Beispiel:
(1) Abgeschlossenheit
Beispiel: 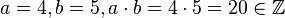 passt.
passt.
(2) Assoziativität
Beispiel: 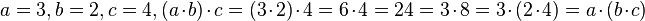 passt.
passt.
(3) neutrales Element
Beispiel: 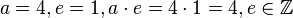 passt.
passt.
(4) inverses Element
Beispiel: 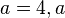 -1
-1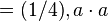 -1
-1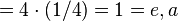 -1
-1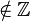 passt nicht!
passt nicht!
Somit handelt es sich bei ![[\Z,\sdot]](/images/math/a/0/3/a037444a418c44fefd7d03f7b97e2d91.png) nicht um eine Gruppe.
nicht um eine Gruppe.

