Gebrochene Zahlen mit der Addition

Wir überprüfen ob $[{\mathbb{\mathbb{Q}}}^{+},+]$ eine Gruppe ist:

Abgeschlossenheit

$\frac{a}{b},\frac{c}{d}\in {\mathbb{\mathbb{Q}}}^{+};a,b,c,d\in {\mathbb{\mathbb{Z}}}^{+};b,d\ne 0$

$\frac{a}{b}+\frac{c}{d}=\frac{a\cdot d}{b\cdot d}+\frac{c\cdot b}{d\cdot b}=\frac{ad+cb}{bd}\in {\mathbb{\mathbb{Q}}}^{+}$
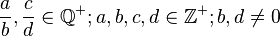
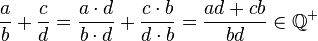
Passt.

Assoziativität

$\frac{a}{b},\frac{c}{d},\frac{e}{f}\in {\mathbb{\mathbb{Q}}}^{+};a,b,c,d,e,f\in {\mathbb{\mathbb{Z}}}^{+};b,d,f\ne 0$

$\frac{a}{b}+(\frac{c}{d}+\frac{e}{f})=(\frac{a}{b}+\frac{c}{d})+\frac{e}{f}$

$\frac{a}{b}+(\frac{cf}{df}+\frac{ed}{fd})=(\frac{ad}{bd}+\frac{cb}{db})+\frac{e}{f}$

$\frac{a}{b}+\frac{cf+ed}{df}=\frac{ad+cb}{bd}+\frac{e}{f}$

$\frac{adf}{bdf}+\frac{bcf+bde}{bdf}=\frac{adf+bcf}{bdf}+\frac{bde}{bdf}$

$\frac{adf+bcf+bde}{bdf}=\frac{adf+bcf+bde}{bdf}$
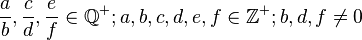
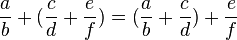
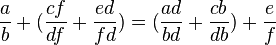
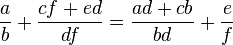
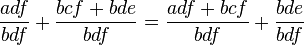
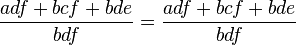
Passt.

neutrales Element

$\frac{a}{b}\in {\mathbb{\mathbb{Q}}}^{+};a,b\in {\mathbb{\mathbb{Z}}}^{+};b\ne 0$

$\frac{a}{b}+n=\frac{a}{b}$

$n=0\in {\mathbb{\mathbb{Z}}}^{+}\in {\mathbb{\mathbb{Q}}}^{+}$
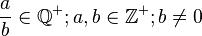
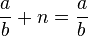
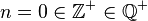
Passt.

inverses Element

$q:=\frac{a}{b};q\in {\mathbb{\mathbb{Q}}}^{+};a,b\in {\mathbb{\mathbb{Z}}}^{+};b\ne 0$

$q+q^{-1}=n=0$

$q^{-1}=\frac{-a}{b}=\frac{a}{-b}=-\frac{a}{b}\notin {\mathbb{\mathbb{Q}}}^{+};-a,-b\notin {\mathbb{\mathbb{Z}}}^{+}$
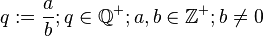
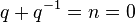
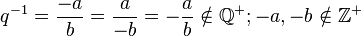
Passt nicht!

Resultat

Somit handelt es sich bei $[{\mathbb{\mathbb{Q}}}^{+},+]$ nicht um eine Gruppe.