GeometrieUndUnterrichtSS2019 06
Vorbereitungsauftrag
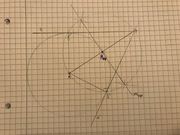
Die Klasse 6a hat gerade gelernt, mit Schnur oder Zirkel Kreise zu zeichnen und weiß, dass „ein Kreis mit Radius 3cm“ aus allen Punkten besteht, die vom Mittelpunkt M genau 3cm entfernt sind. Nun sollen die Kinder einen Punkt finden („konstruieren“), der von A(1;3) genau 7cm und von B(4;1) genau 5cm entfernt ist.
Eine Schüler*in kommt ans Pult. Mit spitzem Bleistift gezeichnet, bietet sie Ihnen voller Stolz in ihrem Heft einen solchen Punkte C an. Sie messen nach, es stimmt. Haargenau! Nur leider sind im Heft der Schüler*in weder Zirkelspuren zu finden noch ein Einstich einer Zirkelspitze.
(adaptiert aus Riemer (2014). „Erziehen im Mathematikunterricht.“ In: Kaenders & Schmidt (Hrsg.) Mit GeoGebra mehr Mathematikverstehen.)
Ergebnisse des Vorbereitungsauftrags
Schreiben Sie auf, wie Sie in dieser Situation reagieren würden.
Reaktion von Wibke
Ich würde den Schüler zuerst loben, dass er die Aufgabe richtig gelöst hat und dabei fragen, wie er auf seine Lösung gekommen ist. Abhängig davon, ob seine Methode in all solchen Aufgaben, die mit Zirkel und Lineal gelöst werden sollen immer funktioniert oder nicht, würde ich ihn motivieren auch den Weg mit Zirkel und Lineal auszuprobieren. Alternativ könnte man den Schüler auch bitten seinen Lösungsweg vor der Klasse vorzustellen und im gleichen Zuge auch einen anderen Schüler bitten, die „herkömmliche“ Methode vorzustellen, damit im Klassengespräch erörtert werden kann, welche Vor- und Nachteile es bei der jeweiligen Methode gibt.
Reaktion von Ilona
In erster Linie würde mich interessieren, wie der Schüler auf die Lösung gekommen ist, da mir intuitiv "nur" die klassische Lösung mit dem Zirkel einfällt. Es wäre möglich, dass der Schüler mehrere Punkte ausprobiert hat, was grundsätzlich auch eine gute Herangehensweise ist, welche ich durchaus unterstützen würde, da sie zeigt, dass der Schüler sich Gedanken über die Aufgabe gemacht und das Prinzip verstanden hat (auch wenn er es nicht in Verbindung mit dem bereits Gelernten bringen konnte). Meiner Meinung nach ist Ausprobieren grundsätzlich eine legtitime Herangehensweise, die jedoch mit zunehmendem thematischem Verständnis obsolet gemacht werden kann. Evtl. könnte man die Klasse vor die Herausforderung einer weiteren Aufgabe stellen, die durch Ausprobieren weniger gut lösbar ist, um zu motivieren, warum uns der Lösungsweg des Schülers nicht ausreicht. Auf jeden Fall würde ich die Richtigkeit der Lösung herausstellen und dann auf den Lösungsweg mit Zirkel hinarbeiten. Möglicherweise ließe sich hier der Lösungsweg eines anderen Schülers vergleichend vorstellen und man könnte entsprechende Vor- und Nachteile erörtern. Die Lösung mit Hilfe des Zirkels wäre dann sozusagen die Verbesserung des Ansatzes des Schülers und zugleich die Verknüpfung mit bereits Gelerntem.
Reaktion von Marc
Ich würde den Schüler zuerst loben und interessiert nach dem Lösungsweg fragen. Hierdurch erfährt die Klasse einen (möglicherweise) alternativen Lösungsweg für das vorgestellte Problem. Im Plenum können mögliche Vor- und Nachteile erörtert werden (Geht es immer? Welcher Ansatz ist schneller, einfacher zu handhaben? …) . Anschließend würde ich den Schüler frage, ob er auch mit dem Ansatz mit Zirkel und Lineal zu einer Lösung gekommen wäre und hierdurch beide Ansätze verstanden hat. Einen alternativen Lösungsweg für eine Aufgabe zu haben, welche zum richtigen Ergebnis führt, ist nicht negativ. Ich persönlich finde es hierbei wichtig auch über den Vergleich der Ansätze zu sprechen und zu vergleichen. Für das Ziel einer Konstruktion mit Zirkel und Lineal müsste die Aufgabe enger gestellt werden.
Reaktion von Katharina
Ebenso wie meine Vorgänger würde auch ich den Schüler zunächst für das richtige Ergebnis loben. Anschließend würde ich ihm erklären, dass es beim Lösen von mathematischen Problemen nicht nur um das Ergebnis, sondern auch um den Lösungsweg geht. Da aus seiner Aufgabenbearbeitung nicht hervor geht, auf welche Art und Weise er zum Ergebnis gekommen ist, wäre es entsprechend schwer, seine Lösungsidee auf ähnlich gestellte Aufgaben anzuwenden. Ich würde den Schüler deshalb in etwa mit den folgenden Worten zu einer erneuten Bearbeitung der Aufgabenstellung ermutigen: „Jetzt versuch einmal die Aufgabe mit einem Lösungsweg so zu bearbeiten, dass alle deine Mitschüler/innen diesen nachvollziehen und genauso gut wie du anwenden können.“
Reaktion von Hajime
Ich würde zuerst den Schüler darum bitten, es uns zu erklären, wie er diesen Kreis gezeichnet hat. Dann würde ich andere Schüler*innen fragen, ob sie andere Lösung gefunden haben und wie er/sie auf die Lösung gekommen ist. Danach würden wir jede Lösung vergleichen, was die Vorteile und Nachteile vom jedem sind, indem wir die Bedingug z.B den Radius ändern.
Reaktion von Patrick
Ein richtiges Ergebnis verdient an erster Stelle ein Lob. Es soll schließlich nicht der Eindruck entstehen, das Ergebnis falsch. Um weiterhin zu erfahren, welchen Lösungsweg der Schüler gewählt hat, frage ich den Schüler nach seinem Vorgehen. Ausgenommen von dem Fall, dass es sich bei dem Schüler um Gauß persönlich handelt, der einen genialen alternativen Weg vorschlägt, ist es wahrscheinlich, dass der Schüler durch glückliches ausprobieren oder eine mentale Abschätzung im Kopf den gesuchten Punkt gefunden hat. Auf die Erklärung "Ich habs einfach ausprobiert", würde ich fragen, ob der Schüler einen konkreteren Weg kennt, welchen er mit garantiertem Erfolg in einer Klassenarbeit anwenden könnte. Im Falle, dass der Schüler sein Ergebnis mit "Ich habs mir vorgestellt" antwortet, wird deutlich, dass der Schüler ein geeignetes Modell im Kopf hat, sich jedoch nicht die Mühe gemacht hat dieses aufzuzeichnen. Um dieses Modell zu festigen und zu validieren würde ich den Schüler auffordern seine Vorstellung zu Papier zu bringen. Hierüber ließe sich das erwartete Verfahren herleiten/motivieren. In beiden Fällen könnte man alternativ zu den genannten Reaktionen fragen, ob es sich bei der gefundenen Lösung um die einzige Lösung handelt und wie man dies herausfinden könnte. Hier würde offensichtlich die Schwäche des "Ich habs ausprobiert"-Verfahrens entlarvt werden. Andererseits könnte dies auch mögliche Fehlvorstellungen oder die Unzuverlässigkeit von rein mentalen Modellen deutlich machen. Im Gegensatz zu diesen Vorgehensweisen bietet die Zirkelmethode eine direkte Antwort auf die Frage. Eine Frage nach der Eindeutigkeit der Lösung bietet darüber hinaus weiteren Diskussionsstoff zum gegebenen Problem.
Reaktion von Anna-Lena
Ich hätte das Ergebnis bestätigt und mich nach seiner Lösungsstrategie erkundigt, um zu erfahren, in wie weit er/sie das zuvor erlernte verinnerlicht hat und welche Problemlösestrategien (willkürliches oder strategisches Ausprobieren, dynamische Überlegungen, Abstrahieren..). Dadurch fühlt sich der/die SchülerIn in seinen Bemühung unterstützt und auch ich bekomme einen Einblick in seine Denk- und Lernprozesse. Gelang er/sie zu der Lösung durch willkürliches Raten (was aufgrund der fehlenden Zirkelstriche der wahrscheinlichste Fall ist), würde ich die Aufgabe erweitern, indem zwei Punkte im Inneren eines Kästchens gewählt werden oder ein nicht kariertes Papier verwendet werden soll. Der/ die SchülerIn ist dadurch gezwungen seine/ihre Strategie zu ändern und das Problem zu abstrahieren. Berichtet er hingegen von einem permanenten Abmessen der Abstände mit dem Geodreieck, enthält die Strategie schon wichtige Ansatzpunkte zur Konstruktion mit Zirkel und Lineal. Hier kann die „Änderung der Lösungsstrategie“ durch eine Genauigkeitsargument motiviert werden: Wie kann ich mir sicher sein, dass der Punkt nicht zufällig ein Millimeter weiter links oder rechts liegt. Als nächster Schritt können reinige richtige Ansatzpunkte seine Strategie genutzt werden, um zur Konstruktion mit Zirkel zu gelangen: Zeichne mir alle Punkte ein die von A 7cm Abstand haben; Er muss also zwei Bedingungen gleichzeitig erfüllen usw. Natürlich kann auch auf letzte Stunde verwiesen werden. Meiner Meinung nach sollte darauf, wenn es das Zeitmanagement erlaubt, verzichtet werden, da, wenn nicht zum Kreis als Lösungsstrategie gegriffen wird, die Grundvorstellung und der Begriff des Kreises nicht vollständig durchdrungen wurde und deshalb weiterer Vertiefung bedarf (v.a. Im Hinblick auf weitere Konstruktionsaufgaben). Ich würde auch nicht das bloße Ergebnis loben, sondern richtige Denkansätze/Lösungsstrategien, da das die eigentlichen Kompetenzen sind. Bei weniger Zeit könnte man auch Ergebnisse an der Tafel sammeln, denn es sind ja zwei Punkte. Wenn kein zweites Ergebnis kommt, könnte man auch selbst die zweite Lösung nennen, die SuS durch messen verifizieren lassen und das Ganze thematisieren: Sind das jetzt alle Lösungen? Sind beide richtig?
Reaktion von Julian
Ich würde den Schüler bitten mir zu zeigen, wie er den Punkt gefunden hat. Anschließend würde ich ihn fragen, ob er eine Methode kennt, mit der man ALLE Punkte finden kann, die die geforderte Eigenschaft erfüllen. Sollte ich davor erklärt haben, was genau unter konstruieren zu verstehen ist, würde ich mit dem Schüler außerdem besprechen, was der Unterschied zu seiner Methode [ohne Zirkel] ist und ob er gegenüber dem Konstruieren Vor-/Nachteile sieht.
Reaktion von Jana
Ich würde ebenfalls zuerst den Schüler für die richtige Antwort loben und anschließend interessiert nach dem Lösungsweg fragen. Zudem würde ich ihm nahebringen, dass er trotz richtiger Antwort, seine Lösung durch die Zirkelvariante kontrolliert und damit Übung auch auf diesem Weg bekommt. Ich würde hinzufügen, dass es in der Zukunft nicht immer nur um die Ergebnisse der S Schüler, sondern auch um den Weg zur Lösung gehen würde und deshalb wichtig ist auch die herkömmliche Methode zu beherrschen, da er sonst bei komplexeren Aufgaben eventuell vor Schwierigkeiten steht.
Sitzungsmaterialien
- Begleitfolien der Sitzung vom 31.05.2019
- Arbeitsblatt zu Grund- und Standardkonstruktionen mit verschiedenen Werkzeugen
Dokumentation der Sitzung
Grundkonstruktionen mit verschiedenen Werkzeugen
Sofern nicht anders angegeben, sind die folgenden Operationen möglich, um eine Ausgangskonfiguration für die Konstruktionsschritte zu schaffen:
- Es können beliebige Punkte in der Ebene gesetzt werden.
- Auf einer Linie (auch Kreislinie) können beliebige Punkte gesetzt werden.
Grundkonstruktionen mit Zirkel und Lineal
- Durch zwei nicht identische Punkte kann eine Lineallinie konstruiert werden. (Gerade)
- Zwischen zwei nicht identischen Punkte kann eine Lineallinie konstruiert werden. (Strecke)
- Zu einer gegebenen Strecke und einem gegebenen Punkt kann kann der Zirkel auf die Streckenlänge eingestellt werden und in dem Punkt eingestochen werden. (Kreis)
- Zu je zwei Objekten von Geraden, Strecken und Kreislinien können die Schnittpunkte konstruiert werden, falls sie existieren.
Grundkonstruktionen mit Papierfalten (Flächen-Origami)
Als Ausgangskonfigurationen dienen hier Faltlinien, sodass in der Ebene beliebige Faltlinien gesetzt werden können.
- Zu zwei nicht parallelen Faltlinien kann der Schnittpunkt konstruiert werden.
- Durch zwei nicht identische Punkte kann eine Faltlinie konstruiert werden.
- Zu zwei Punkten kann eine Faltlinie so konstruiert werden, dass die zwei Punkte aufeinander gefaltet werden.
- Zu zwei Linien kann eine Faltlinie so konstruiert werden, dass die zwei Linien aufeinander gefaltet werden.
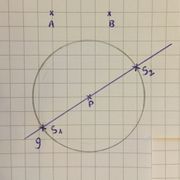
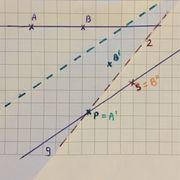
- Gegeben seien zwei Punkte M und P sowie eine Linie g. Dann kann eine Faltlinie durch M so konstruiert werden, dass P auf g gefaltet wird. (Schnitt von Kreis und Gerade)
- Gegeben seien zwei Punkte P und Q sowie zwei Geraden g und h, sodass nicht gleichzeitig P auf g, Q auf h und g parallel zu h liegt. Dann kann eine Faltlinie konstruier werden, sodass P auf g und Q auf h gefaltet wird. (Einschiebelinieal)
Zusammenfassung
Im Ersten Teil dieser Sitzung wurde die Bedeutung des Konstruierens im Geometrieunterricht beleuchtet. Später wurde die Abhängigkeit der Konstruktion von den verwendeten Werkzeugen, sowie die Hierarchie der Konstruktionsschritte betrachtet.
Einstieg
Zunächst wurde in einem Zumpad Dokument gesammelt wozu Konstruktionen im Geometrieunterricht dienen können.
Vergleiche: https://zumpad.zum.de/p/GuU_Konstruktion
Konstruktionen dienen…
- … zur Förderung von Problemlösekompetenzen
- … zur Vertiefung von Begriffsverständnissen
- … als Möglichkeit im Mathematikunterricht Beweise zu führen, was in anderen Gebieten der Schulmathematik schwierig zu bewerkstelligen ist. Dabei dienen Konstruktionen als Existenzbeweise (Vergleiche Vorbereitungsauftrag: Ist der gefundene Punkt der Einzige der die Bedingung erfüllt?) oder Verifikationsbeweise (Erfüllt die gefundene Lösung die Bedingungen).
- ... Zur Förderung motorischer Fähigkeiten (Umgang mit Werkzeugen)
- ... Zur Veranschaulichung abstrakter Zusammenhänge
Bedeutung des Konstruierens
Im nächsten Teil wurde die Bedeutung des Konstruierens im Unterricht aufgearbeitet (Vergleiche Folien 3-5).
Funktionen
Konstruieren im Geometrieunterricht kann folgende Funktionen erfüllen:
- Entdecken geometrischer Zusammenhänge
- Entdeckung von Beweisideen: durch Durchführung von Konstruktionen
- Kulturhistorische Bedeutung: „Werkzeuge der alten Griechen“
- Entwicklung und Förderung von Problemlösefähigkeiten: Für Konstruktion zulässige Werkzeuge und Operationen sind leicht zu verstehen und zu handhaben; einzelne Lösungsschritte lassen sich gut nachvollziehen, verbalisieren und verschriftlichen.
- Entwicklung und Förderung von Argumentationsfähigkeiten: Konstruktionsaufgaben bieten klare Argumentationsbasis; Lösungen lassen sich schrittweise entwickeln und Begründen
- Handlungsbezogene Begriffsbildung: Begriffseinführung über Konstruktionen (z.B.: Drache, Parallelogramm, Mittelsenkrechte)
- Training von Zeichenfähigkeit und Feinmotorik: Erziehung im sorgfältigen Umgang mit Zirkel und Lineal; Möglichkeit zur Differenzierung z.B. Zugang zu unterschiedlichen Werkzeugen (Geodreieck als Abkürzung)
Standards
Es wurde sich mit den Bildungsstandards auseinandergesetzt (vgl. Folie 4). Dabei wurde gerade das gedankliche operieren mit geometrischen Begriffen und der unterschied zwischen zeichnen und konstruieren von geometrischen Figuren hervorgehoben. Beim Konstruieren geht es nicht vorrangig um das tatschliche Herstellen realer Objekte, sondern um das gedankliche Erzeugen ideeller Objekte ( Punkte ohne Ausdehnung, Strecken ohne Breite) mithilfe idealisierter Operationen (Kreise ziehen, Punkte mit Lineal verbinden) (vgl. Wiegand et al. 2018, S. 51). Statt nur zum Zeichnen werden Konstruktionen zur Beurteilung und Untersuchung von Problemstellungen angewendet. Zur Leitidee „Raum und Form“ kam im Seminar die Frage auf, ob perspektivisches Zeichnen Konstruieren ist.
Mathematisch
Es wurde sich nochmals mit dem Unterschied zwischen dem Herstellen von realen Objekten und dem Konstruieren von ideellen Objekten beschäftigt. Konstruieren führt in der Vorstellung zu theoretisch exakten Ergebnissen, die praktisch, auch durch größtmögliche Sorgfalt der Konstruktion, nur innerhalb einer Zeichentoleranz genau sein können. Tatsächliche Realisierungen der (idealen) Konstruktion sind stets nur Näherungen.
Konstruieren bedeutet eine vorgegebene Ausgangskonfiguration durch Einsatz ausgewählter Werkzeuge, die nur nach festgelegten Regeln genutzt werden dürfen, eine Zielkonfiguration zu erzeugen. Zu gegebener Ausgangskonfiguration kann es keine, genau eine oder mehrere Zielkonfigurationen geben
- Ausgangskonfiguration: Eine Menge geometrischer Objekte (z.B. Punkte, Kreise, Geraden) und ein System von Beziehungen (z.B. der Punkt A liegt auf Gerade g).
- Konstruktionsschritte: Eine endliche Anzahl von Operationen mit festgelegten Werkzeugen (z.B. Zirkel und Lineal), die nur nach festen Regeln verwendet werden. So dürfen z.B. mit dem Lineal nur zwei gegebene Punkte verbunden werden, und ein Kreis kann nur bei gegebenem Mittelpunkt und einem Kreispunkt bzw. gegebenem Radius gezeichnet werden.
- Zielkonfiguration: Diese ist – falls sie existiert – wieder eine Menge geometrischer Objekte und Beziehungen, die die Ausgangskonfiguration einschließt und erweitert.
Besprechung des Vorbereitungsauftrags
Anschließend wurde der Vorbereitungsauftrag besprochen (vgl. oben). Hier einige Gesprächsbeiträge:
Als Erste Reaktion hat sich ein Lob für die Lösung herauskristallisiert. Eine anschließende Nachfrage wie der Punkt gefunden wurde war für alle Teilnehmer essentiell. Falls die Lösung durch Ausprobieren gefunden wurde, gab es den Vorschlag die Systematik der SchülerIn zu erfragen. Hier kann klargestellt werden das systematische Ausprobieren ein valider Lösungsansatz ist, aber auch dessen Grenzen lassen sich erkennen. Ohne Lösungsweg wird jede neue Aufgabe durch neuerliches, langwieriges Ausprobieren (falls überhaupt) gelöst. Um die SchülerIn von der Nutzung von Konstruktionsschritten zu überzeugen, lassen sich kritische Fragen stellen, z.B. „Sind das alle Punkte die die Aufgabe erfüllen?“, „Wie würdest du Alle finden?“, „Ist ausprobieren der bessere Weg?“. Ein Vorschlag war für die Aufgabe unterschiedliche Lösungswege zu sammeln und in der Klasse als soziale Gruppe eine Einigung über den sinnvollsten Lösungsweg zu suchen.
Es wurde noch festgehalten, dass zu jeder Konstruktionsaufgabe, eine Konstruktionsbeschreibung angefertigt werden muss. Diese enthält eine nachvollziehbare, vollständige Beschreibung der Konstruktionsschritte und ist dem sprachlichen Niveau der Lernenden angepasst. Sie entwickelt sich von zunächst umgangssprachlichen Formulierungen zu einer zunehmend formalisierten Darstellung weiter. Der Nutzen eine Konstruktionsbeschreibung ist vielfältig.
Konstruktionsbeschreibungen…
- ... Stellen für Lernende eine Dokumentation des eigenen Lösungsweges dar.
- ... Erlauben Kontrolle des Lösungsweges für Lernende und Lehrende.
- ... Erlauben ein Nachvollziehen der Konstruktion auf Zeichenebene
- ... Dienen zur Kommunikation im Unterricht
Konstruktionsschritte und Werkzeuge
Konstruktionsschritte sind Operationen die innerhalb einer Konstruktions angewendet werden können. Sie sind abhängig von den verwendeten Wekzeugen und lassen sich in Grundkonstruktionen, Standardkonstruktionen und Modulkonstuktionen unterteilen.
Grundkonstruktionen sind Konstruktionen, die mit dem jeweiligen Werkzeug in einem Schritt erzeugt werden können.
- „Axiomsystem“ für Lösung von Konstruktionsprobleme
- Abhängig von erlaubten Werkzeugen
Standardkonstruktionen sind die Zusammenfassung mehrerer Grundkonstruktionen
- Pragmatische Festlegung durch Häufigkeit und Bedeutung
- Festlegung wurde auch sozial ausgehandelt
Mit Zirkel und Lineal sind beispielsweise
- einen Kreis mit Mittelpunkt A durch B zeichnen
- eine Gerade durch die Punkte A und B zeichnen
- eine Halbgerade ausgehend von Punkt A durch B zeichnen
- die Strecke [AB] zeichnen
Grundkonstruktionen. Wird ein Geodreieck verwendet so sind auch das Zeichnen von Senkrechten und Parallelen, sowie das Abtragen von Winkeln Grundkonstruktionen. Gerade die Konstruktion von Senkrechten und Parallelen sollten mit Zirkel und Lineal zu Standardkonstruktionen werden.
Übung
Um das Anfertigen von Konstruktionsbeschreibungen zu üben und um die Abhängigkeit der Konstruktionsaufgabe vom erlaubten Werkzeug zu erfahren, wurde das Arbeitsblatt zu Grund- Standardkonstruktionen bearbeitet (siehe Oben).
Modulkonzept
Modulkonstruktionen sind die Zusammenfassung mehrerer Konstruktionsschritte, die als Ganzes betrachtet werden.
- Pragmatische Festlegung durch Häufigkeit und Bedeutung
- Festlegung wurde auch sozial ausgehandelt
Modulkonstruktionen können mental in einem Schritt ausgeführt werden
- Modulkonstruktionen sind mentale Grundkonstruktionen
- Modulkonstruktionen sind Grundkonstruktionen von komplexen Werkzeugen
Beispiel für Modulkonstruktionen die gedanklich in einem Schritt durchgeführt werden können, wäre die Konstruktion von Kongruenten Dreiecken. Das Geodreieck ist ein Komplexes werkzeug mit dem Parallelen und Senkrechten, Grundkonstruktionen sind. Modulkonstruktionen sind Voraussetzung für komplexe Konstruktionsaufgaben, indem Sie eine kompakte Konstruktionsbeschreibung erlauben („Ich konstruiere die Mittelsenkrechte“). Sie bilden ein Abbild der mathematischen Denk- und Arbeitsweise. Mathematische Sätze, Lemmas, usw. werden (einmal bewiesen) als Teile in anderen Beweisen eingesetzt, ohne deren Beweise jedes Mal wieder aufzuzeichnen. Hier wird klar, dass Modulkonstruktion zunächst erarbeitet (Bewiesen/Motiviert) und aufgebaut werden müssen (White-Box-Prinzip).
Nachbereitungsauftrag
- Suchen Sie sich eine der unten stehenden Konstruktionsaufgaben aus, in dem Sie Ihren Namen in die Überschrift eintragen.
- Lösen Sie die Konstruktionsaufgabe mit den angegebenen Hilfsmitteln (Zirkel und Lineal, Geodreieck, Papierfalten). Für die Faltkonstruktionen können Sie u.a. Paulus (2018) „Geometrische Konstruktionen und Origami“ zur Hilfe nehmen.
- Fertigen Sie jeweils eine Planskizze und eine Konstruktionsbeschreibung an und tragen Sie diese in die unten stehende Tabelle ein.
- Entwerfen Sie ein GeoGebra-Applet, in dem Sie Ihre Konstruktion realisieren. Erstellen Sie ausgehend von Ihrer Konstruktion ein „GeoGebra-Werkzeug“ für die Konstruktionsaufgabe. Verlinken Sie in der Tabelle das Applet in der Gestalt, dass nur die Ausgangskonfiguration sichtbar ist und nur Ihr erstelltes Werkzeug auswählbar ist.
Das Modulkonzept kann direkt in GeoGebra umgesetzt werden. Dazu können Werkzeuge ausgeblendet werden, sodass etwa nurnoch Grundkonstruktionen verfügbar sind. Es können auch eigene Werkzeuge (Module, Markros) erstellt werden. Die Bedienung habe ich kurz von meinem Bildschirm abgefilmt und hier verfügbar gemacht. Sie können in der GeoGebra-Anleitung nachlesen, wie Sie die Werkzeugleiste anpassen und wie Sie eigene Werkzeuge erstellen können.
Gegebene Strecke auf Gerade abtragen (wird bearbeitet von: Katharina)
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze | |||
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
https://www.geogebra.org/graphing/bxak7bcp Eigenes Werkzeug: https://www.geogebra.org/classic/zkkysctm |
Link zu GeoGebra Aktivität |
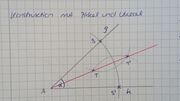
Gegebenen Winkel auf Gerade abtragen (wird bearbeitet von: Lukas)
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
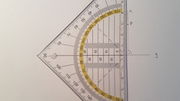
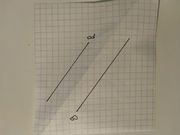
| Planskizze |
Bild |
Bild |
Bild |
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Mittelpunkt einer Strecke (wird bearbeitet von: Marc )
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
Bild |
Bild |
Bild |
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
https://wiki.geogebra.org/de/Mittelsenkrechte_%28Werkzeug%29 https://wiki.geogebra.org/de/Schneide_(Werkzeug) |
https://www.geogebra.org/classic/tjrbpwmf (Eigenes Werkzeug) |
Link zu GeoGebra Aktivität |
Kommentar des Dozenten:
- Der Radius r ist nicht spezifiziert und es ist daher unklar, ob die Schnittpunkte überhaupt existieren. Zur Erinnerung: Es können nur Streckenlängen auf dem Zirkel eingestellt werden, die bereits konstruiert sind und sich daher abtragen lassen.
- Bei Anwendung des Konstruktionswerkzeugs werden auch die Kreise mitkonstruiert.
Winkelhalbierende (wird bearbeitet von: Ilona)
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze | |||
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Schnittpunkt von Kreis und Gerade (wird bearbeitet von: )
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
Bild |
Bild |
Bild |
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Das Lot zu einer Geraden durch gegebenen Punkt (wird bearbeitet von: Wibke )
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze | |||
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Parallele zu Gerade durch gegebenen Punkt (wird bearbeitet von: )
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
Bild |
Bild |
Bild |
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Mittelparallele (wird bearbeitet von: Julian)
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze | |||
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
„Einschiebeineal“ (wird bearbeitet von: )
Gegeben seien jeweils verschiedene Punkte P und Q und Geraden p und q, so dass nicht gleichzeitig P ∈ p, Q ∈ q und p || q gilt. Dann kann man so falten, dass P auf p und Q auf q zu liegen kommt.
Konstruktionen mit dem Einschiebelineal:
- Unter einem Einschiebelineal versteht man ein Lineal, auf dem zwei Punkte P, Q markiert sind, somit ist eine bestimmte Streckenlänge auf diesem Lineal fixiert. Man kann das Lineal so verschieben, dass diese Punkte auf bestimmten Geraden (oder Kreisen) liegen.
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
(Nicht möglich.) |
Bild |
Bild |
| Konstruktionsbeschreibung |
(Nicht möglich.) |
|
|
| GeoGebra |
(Nicht möglich.) |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
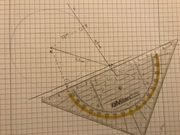
Tangente an einen Kreis durch gegebenen Punkt (wird bearbeitet von: Anna-Lena)
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
Bild | ||
| Konstruktionsbeschreibung |
Ausgangskonfiguration 1: Kreis mit Mittelpunkt M und Radius R und einen beliebigen Punkt P.
Ausgangskonfiguration 2: Kreis mit Mittelpunkt M und Radius R und der Punkt P liegt auf dem Kreis.
|
Ausgangskonfiguration 1: Kreis mit Mittelpunkt M und Radius R und einen beliebigen Punkt P.
Ausgangskonfiguration 2: Kreis mit Mittelpunkt M und Radius R und der Punkt P liegt auf dem Kreis.
|
Ausgangskonfiguration (?): Kreis mit Mittelpunkt M und Radius R und einen beliebigen Punkt P.
Ausgangskonfiguration 2: Mittelpunkt M und der Kreispunkt P ist gegeben.
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Rechtwinkliges Dreieck mit vorgegebenen Kathetenlängen (wird bearbeitet von: )
| Konstruktion mit Zirkel und Lineal | Konstruktion mit Geodreieck | Konstruktion mit Papierfalten | |
|---|---|---|---|
| Planskizze |
Bild |
Bild |
Bild |
| Konstruktionsbeschreibung |
|
|
|
| GeoGebra |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Link zu GeoGebra Aktivität |
Literaturhinweise
- Paulus (2018). „Geometrische Konstruktionen und Origami“. (arXiv, Abschlussarbeit)
- Kaenders & Schmidt (2014). „Mit GeoGebra mehr Mathematikverstehen“






 und
und  gegeben.
gegeben.
 auf
auf 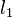 . [siehe
. [siehe  uder Gerade
uder Gerade  . [siehe
. [siehe 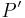 .]
.]