GeometrieUndUnterrichtSS2019 09
Inhaltsverzeichnis |
Vorbereitungsauftrag
Lesen Sie Prediger & Hein (2017). Learning to meet language demands in multi-step mathematical argumentations: Design Research on a subject-specific genre. In European Journal of Applied Linguistics 5(2). Beantworten Sie für sich die folgenden Fragen/Aufgaben.
Fragen zu den Abschnitten 1 und 2
- Welche Schwierigkeiten oder Anforderungen bestehen beim Beweisen und Argumentieren für Schülerinnen und Schüler?
- Was halten Sie für die größte Anforderungen? Was war für Sie die überraschendste Schwierigkeit?
Fragen zu den Abschnitten 3, 4 und 5
- Welcher Ausschnitt aus den empirischen Daten (Aussage in einem SuS-Dialog, Auszug aus einem SuS-Text, …) war für Sie überraschend oder besonders interessant?
- Wählen Sie einen beliebigen Beweis aus der Geometrie aus und bereiten Sie ihn in der im Artikel vorgestellten Strukur (Figure 8) auf.
Sitzungsmaterialien
Dokumentation der Sitzung
Zusammenfassung
Die Ergebnisse des Vorbereitungsauftrages wurden besprochen und das im zu lesenden Paper erörterte "scaffolding" erörtert. Anschließend wurde dieses am konkreten Beispiel des Beweises des Satz des Thales aufzubereitet.
Besprechung des Vorbereitungsauftrages
Zur Vorbereitung der Sitzung war das Paper „Learning to meet language demands in multi-step mathematical argumentations: Design Research on a subject-specific genre“ (Prediger & Hein, 2017) zu lesen. Zu Beginn der Sitzung wurde dieser besprochen und die einzelnen Kapitel bzw. Textblöcke analysiert. Ziel des Papers war es, sich mit Schwierigkeiten von SuS auseinanderzusetzen, die bei(m Aufbau von) Argumentationen bzw. Beweisen in der Mathematik auftreten können und wie diese behoben werden könnten. Diese wurden an der Tafel festgehalten:
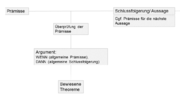
Probleme bei Beweisaufgaben im Unterricht
- Unterscheidung von Prämissen, Argument, Argument in Anwendung, Schlussfolgerung
- Einsichtigkeit der (Allgemein)Gültigkeit von Aussagen, sowie die Möglichkeiten der Anwendung zu begreifen und diese „parat zu haben“
- Konkrete Beispiele (Experimentelles Beweisen) als nicht-ausreichend akzeptieren
- Fehlendes Beweisbedürfnis
- Wenn-dann („if-then“) einsehen („Understanding their structure is crucial for avoiding circularity”)
- Prämissen zur Anwendung explizit prüfen (Im Alltag würden diese nur formuliert, falls die entsprechende Prämisse zutrifft)
- Mangelnde „sprachliche Bausteine“, um logische Strukturen/Abfolgen auszudrücken
- Inhaltlose Verwendung von „Worthülsen“, wie „Ohne Beschränkung der Allgemeinheit“, „Es sei…“, „Es gilt/ Es gelte“, da diese u.U. nicht begriffen wurden
Während in der Sitzung mehrere Forschungskonzepte genannt wurden, konzentrierte sich die Sitzung auf den Ansatz der Studie, welche im obigen Paper durchgeführt wurde. Dieser basierte auf „structural scaffolding“. Dies hat den Ansatz kognitive Ansprüche zu entlasten und anschließend Vorgaben und Hilfen bezüglich der Struktur/Strukturfindung abzubauen, um den SuS den Aufbau, Inhalt und Struktur sowie Sprache eines (mathematischen) Beweises näherzubringen. Als Beispiel wurden Lückentexte genannt, bei denen zuerst nur noch wichtige Argumente einzusetzen sind, allerdings im weiteren Verlauf die Lücken stetig vergrößert werden. Zur Abfolge der Argumentation in Abb.1 wurde diskutiert, ob diese bei komplexeren Beweisen durch ihre zwangsläufig rekursive Struktur (Für die eigentliche Aussage müssen ggf. innerhalb des Beweises zunächst andere Aussagen gezeigt werden) nicht zu uneinsichtig für SuS sein dürften. Das Ergebnis war, dass man sich stets überlegen müsse, welche Beweise sich überhaupt für die Methode eignen und an welcher Stelle der Schullaufbahn das scaffolding idealerweise eingesetzt werden sollte. Letztlich sei es eher ein Werkzeug für Beweise mit wenigen Schritten.
Diskussion der Durchführung/Ergebnisse der Studie
Die Grundidee des scaffolding wurde positiv wahrgenommen, ebenfalls das konkrete Beispiel, welches in der Studie verwendet wurde („vertically opposite angle theorem“), allerdings wurde hinterfragt, ob in der Realität die Anwendung tatsächlich gewinnbringend sein dürfte, da zumal auch von den Autoren aufgeführt wurde, dass die alleinige Behandlung dieses Beweises keine weitläufigen Aussagen zulasse (chapter 5 : „This study has methodological limitations that will still have to be overcome in later design experiment cycles or future research. […] The teaching-learning arrangement focused only on angle theorems; future research should extend to other topics”). Ebenfalls wurde angemerkt, dass hier eventuell das Augenmerk zu stark auf der Struktur liege, sodass der eigentliche Beweis in den Hintergrund gerate. Allerdings sei aber auch das Lernziel die Fähigkeit Differenzierbarkeit von Prämisse, Argument usw., sowie die sprachliche Struktur und Beweisstruktur zu unterstützen.
Des Weiteren wurde bemerkt, dass die Verwechslung der SuS im Text zum Teil ihren Ursprung daran haben könnte, da innerhalb des Unterrichtes bei Abfragen bzw. Rückfragen an die SuS die Lehrkräfte häufig mit knappen Antworten zufrieden seien, sodass eine strukturierte Begründung seitens der SuS selten vorkomme (Bsp.: L: „Woran liegt das?“ S: „Pythagoras.“ L: „Richtig.“) Auch wurde der Unterschied zwischen mündlicher und schriftlicher Beweisstruktur wahrgenommen, wobei dieser ggf. bei mündlicher Abfrage an der Unsicherheit, wie die Antworten aussehen sollen liegen könne, sowie der Tatsache, dass bei der schriftlichen Verfassung erst nach der mündlichen erfolgte, sodass eine Reflexion seitens der Sus erfolgen konnte.
Inputphase
In dieser Phase wurde an die vorherige Stunde angeknüpft, indem zunächst der Text zentral zusammengefasst und ggf. ergänzt wurde. Es wurden verschiedene Motivationen von Beweisen erörtert, wie Einsichtigkeit der Allgemeingültigkeit der Aussage oder diese zu veranschaulichen.
Auch wurde Beweisen an sich differenziert betrachtet unter der Beweisfindung (Problem lösen) und der Beweisdarstellung (Bsp.: scaffolding), die beschreibend oder symbolisch erfolgen kann. Hierbei erfolgt die Beweisfindung eher als kreativer Prozess, der sprunghaft sein kann und auch Rückschläge in sich birgen kann, während die Darstellung lediglich die Präsentation des Ergebnisses ist, welche an das jeweilige Publikum angepasst wird und formalen Kriterien genügt. Anschließend wurde der Idealtypischer Beweis-Prozess (nach Boero) vorgestellt, sowie wie dies bei SuS angewendet werden kann und welche Probleme auftreten können [ für Details: s. Sitzungsmaterialien]. Hier wurde betont, dass es wichtig sei, bei SuS ein Beweisbedürfnis zu wecken und diese zu motivieren.
Arbeitsphase
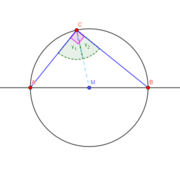
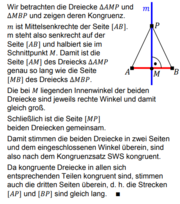
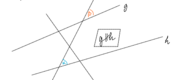
Abschließend zur Sitzung wurde das Gelernte genutzt, um den Beweis für den Satz des Thales für SuS aufzubereiten. Die erste Formulierung: „Alle Winkel an einem Halbkreis sind rechte Winkel“ wurde zunächst formal bewiesen:
Formaler Beweis
Es ist
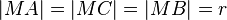 ,
,
wobei r den Radius des Kreises bezeichnet. Also sind ΔAMC und ΔMBC gleichschenklig. Insbesonders gilt aufgrund des Basiswinkelsatzes für gleichschenklige Dreiecke:
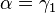 und
und 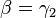 .
.
Wegen des Satzes der Winkelsumme im 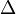 gilt:
gilt:
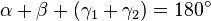
und mit
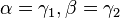
ergibt sich
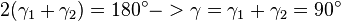 .
.
Aufbereitung des Beweises
Zunächst stellte sich die Frage, welches Vorwissen bei den SuS vorhanden sein und aktiviert werden muss. Dies wurde an der Tafel zusammengetragen:
- Alle Punkte auf einer Kreislinie haben den gleichen Abstand zum Kreismittelpunkt
- Basiswinkelsatz für gleichschenklige Dreiecke
- Satz über Winkelsumme im Dreieck, Rechnen mit Winkeln (Addierbarkeit, Ergänzung von Winkeln)
- Lösungsverfahren von Gleichungen, speziell Einsetzungsverfahren
- Definition & Eigenschaften von gleichschenkligen Dreiecken
Anschließend wurde diskutiert, wie man dieses Vorwissen aktivieren könne, im Hinblick auf den möglichen Zeitaufwand zu Beginn einer Unterrichtsstunde. Genannt wurden Besprechung von Hausaufgaben, Kurzteste oder -abfragen sowie ein Quizz zu beginn. Für letzteres sollten Fragen entworfen werden, die im Idealfall aus Zeitgründen kompakt, aber dennoch alles abdecken sollten. Beispiele waren:
- Was ist ein Kreis?
- Was ist ein (gleichschenkliges) Dreieck?
- Wieviele rechte Winkel kann ein Dreieck haben?
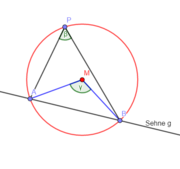
Allerdings wurden auf den Einwand hin, dass eventuell Schwierigkeiten dabei auftreten könnten, den Bezug dieses Wissen zum Beweis zu sehen, noch bildliche Beispiele genannt, die in Richtung der obigen Skizze des Beweises gingen. Hierbei könnte man fragen: "Wie lang ist |AB|?" usw.
Nachbereitungsauftrag
Entwerfen Sie eine Prüfungsfrage bzw. ein kurzes Prüfungsgespräch zu den Sitzungen zum Beweisen & Argumentieren (I+II). Ihre Frage sollte dabei nicht nur bloße Wissensabfrage sein, sondern auch Anwendungen, Begründungen oder Diskussionen erfordern. (Sollte Ihnen doch nur Aufgaben zur bloßen Wissensabfrage einfallen, entwerfen Sie drei Prüfungsfragen.)
- Formulieren Sie Ihre Prüfungsfrage bzw. den Anlass für das Prüfungsgespräch in der Aufgabenstellung-Spalte.
- Beschreiben Sie ausführlich, wie mögliche (richtige) Antworten auf Ihre Frage aussehen könnten bzw. welche Aspekte in einem Prüfungsgespräch zu dieser Frage angesprochen werden sollten. Tragen Sie dies entsprechend in die Erwartungshorizont-Spalte ein.
- Erläutern Sie kurz, warum Sie diese Aufgabe einen zentralen Aspekt der Sitzung abdeckt und welche Anforderung an Wissen/Kompetenzen die Aufgabe fordert.
Unter den übergreifenden Literaturhinweise sind insbesondere relevant:
- Blum & Kirsch (1991). Preformal Proving: Examples and reflections. In Educational Studies in Mathematics.
- Meyer & Prediger (2009). Warum? Argumentieren, Begründen, Beweisen (Preprint). In Praxis der Mathematik in der Schule 51(30).
- Prediger & Hein (2017). Learning to meet language demands in multi-step mathematical argumentations: Design Research on a subject-specific genre. In European Journal of Applied Linguistics 5(2).
- Kapitel 2 „Beweisen und Argumentieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“
- Abschnitte: „Was ist ein Beweis?“, „Funktionendes Beweisens“, „Beweis und Beweisfindung“
- Abschnitte: „Kompetenzen vonSchülerinnen und Schülern“, „Inhaltlich-anschauliche Beweise“
- Präsentationsfolien zu Kapitel 4 „Beweisen und Argumentieren“ der Vorlesung „Didaktik der Mathematik in der Sek. I / Didaktik der Geometrie“. In Vorlesungsskripte von Jürgen Roth, Universität Koblenz-Landau.
Ergebnisse der Nachbereitung
Tragen Sie die Ergebnisse Ihrer Nachbereitung in die folgende Tabelle ein.
| Aufgabenstellung | Erwartungshorizont | Diskussion |
|---|---|---|
|
|
Bei der Beantwortung dieser Fragen beschäftigen sich die Studierenden mit dem Begriff des Scaffoldings, welcher fächerübergreifend von zentraler Bedeutung ist. Darüber hinaus werden die grundlegenden Vorgehensweisen der Unterrichtsplanung wiederholt und die Studierenden dazu aufgefordert, das Prinzip des Scaffoldings explizit in die Überlegungen mit einzubeziehen. |
|
Betrachten Sie die folgenden beiden Beweismöglichkeiten. |
|
Durch diese Aufgabe werden verschiedene Beweisdarstellungen wiederholt und an einem konkreten Beispiel aufgezeigt. Vor-und Nachteile werden diskutiert, um die Beweisdarstellungen gegenüberzustellen. |
|
Eine SchülerIn formuliert folgenden Beweis zum Satz über die Winkelhalbierenden im Dreieck: "Ich konstruiere die Winkelhalbierende w_α von α. Jeder Punkt auf w_α ist gleich weit von b und c entfernt. Das Heißt, ich kann einen Kreis mit Mittelpunkt auf w_α konstruieren, der b und c jeweils in einem Punkt schneidet. Wenn ich den Mittelpunkt des Kreises auf w_α verschiebe, dann berührt der Kreis irgendwann die Seite a. Also hat jedes Dreieck einen Innenkreis." Beurteilen Sie den vorliegenden Beweis. Wie könnte eine Rückmeldung an die SchülerIn aussehen? |
Eine Rückmeldung muss auf die Unvollständigkeit des vorliegenden Beweises hinweisen. Dies kann durch Fragen geschehen, die auf die Nutzung aller gegebenen Voraussetzungen (alle Winkelhalbierenden) abzielen ("Was passiert wenn du deine Überlegungen auf die anderen Winkel/Winkelhalbierenden anwendest?"). Das sich der Beweis nicht als Konstruktionsbeschreibung für die Konstruktion eines Innenkreises eignet, kann auch Anlaß bieten um der SchülerIn die mangelnde Qualität ihres Beweises aufzuzeigen. |
Durch diese Aufgabe werden Problematiken die SchülerInnen mit Beweisen und Argumentieren haben können angesprochen. |
|
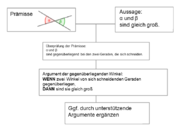
In einem Interview mit Schülerinnen und Schülern der Jahrgangsstufe 8 wird den Befragten die Aufgabe gestellt, den Winkelsummensatz („Die Winkelsumme der Innenwinkel eines Dreiecks beträgt 180°) zu beweisen. Als Hilfestellung erhalten sie die Skizze eines Dreiecks, in welche bereits die Innenwinkel α, γ und β, eine zur Seite AB parallele Gerade g mit C ∈ g und die Wechselwinkel α* von α und β* von β eingezeichnet sind. Betrachten Sie die Vorgehensweisen von Oliver. Welche Schwierigkeiten beim Argumentieren und Beweisen zeigen sich? Wie könnten Sie als Lehrperson diesem Problem entgegenwirken? Olivers Vorgehensweise: Oliver geht bereits von der Winkelsumme im Dreieck aus und argumentiert, dass aus α + γ + β = 180° und α* + γ + β* = 180° die zu beweisende Behauptung α* = α und β* = β folgt. Schlussendlich argumentiert er: „Weil, wenn es weniger als 180° wäre, dann würde das Dreieck überhaupt nicht zusammenpassen. Es gibt kein Dreieck, was nicht 180° hat.“ |
Der gröbste Fehler in Olivers Argumentationsweise ist, dass er mehrmals die zu beweisende Aussage benutzt. Die Unterscheidung zwischen Prämissen und Schlussfolgerungen gelingt ihm offensichtlich nicht. Für die Schlussfolgerung, dass aus den Gleichungen α + γ + β = 180° und α* + γ + β* = 180° die Gleichheiten α* = α und β* = β folgen, liefert er kein Argument. Wesentliche Vorkenntnisse und Fertigkeiten beim Umgang mit Gleichung scheinen ihm zu fehlen. Aus der „Erfahrung“, dass er kein Dreieck kennt, dessen Innenwinkelsumme nicht 180° beträgt, folgert er, dass dies für alle, d.h. für allgemeine Dreiecke gilt. Er sieht also nicht ein, dass empirische Argumente für mathematische Beweise keine ausreichende Gültigkeit besitzen. Um dem gröbsten Argumentationsfehler von Oliver, dem Verwenden des zu beweisenden Satzes, entgegenzuwirken und die Unterscheidung von Prämisse, Argument und Schlussfolgerung zu fördern, könnte das Argumentationsmodell von Toulmin im Unterricht eingesetzt und den Schülerinnen und Schülern bei Beweisaufgaben als Hilfestellung zur Hand gegeben werden. Wesentliches Merkmal dieses Modells ist die spezifische Unterscheidung von Prämisse, Argument und Schlussfolgerung. |
Mithilfe dieser Aufgabe können die Schwierigkeiten von Schülerinnen und Schülern beim mathematischen Argumentieren und Beweisen beispielhaft deutlich gemacht und mögliche Maßnahmen für Lehrpersonen diskutiert werden. |
|
Klasse 7, Behauptung: In einem Trapez ergeben zwei auf der derselben Seite eines Schenkels liegenden Winkel zusammen 180°.
|
|
In der Aufgabe muss das Toulmin-Schema angewandt werden und über Schülervoraussetzungen und Hilfestellung bei der Beweisfindung reflektiert werden. Zuletzt werden auch die Funktionen von Beweisen auf ein konkretes Beispiel übertragen und Umsetzungsmöglichkeiten zum Wecken des Beweisbedürfnis genannt. |
|
Sie planen verschiedene Aktivitäten zum Beweis des Satzes über die Winkelsumme im Dreieck. Erklären Sie die Unterschiede zwischen einem experimentellen Beweis, einem inhaltlich-anschaulichen Beweis und einen formalen Beweises anhand dieses Satzes. Wie könnte differenziertes Arbeitsmaterial zu diesem Themengebiet aussehen? |
Ein experimenteller Beweis verwendet meist Alltagssprache und zeigt (meist) nicht die Allgemeingültigkeit eines Satzes. In diesem Kontext könnten die SuS verschiedene Dreiecke mit dem Geodreieck vermessen und so feststellen, dass die Winkelsumme immer 180° ist. |
In der Aufgabe müssen die Begriffe experimenteller Beweis, inhaltlich-anschaulicher Beweis und formaler Beweis erklärt werden. Desweiteren müssen diese Begriffe in Zusammenhang mit einem konkreten Satz aus der Schulmathematik gebracht werden. Außerdem sollen konkrete Vorschläge der Umsetzung für den Unterricht vorgeschlagen werden. |
Literaturhinweise
- Prediger & Hein (2017). Learning to meet language demands in multi-step mathematical argumentations: Design Research on a subject-specific genre. In European Journal of Applied Linguistics 5(2).
- Kapitel 2 „Beweisen und Argumentieren“ in Weigand et. al. (2018). „Didaktik der Geometrie für die Sekundarstufe I“. Insbesondere Abschnitt „Kompetenzen vonSchülerinnen und Schülern“.