Innen- und Außenwinkelsatz für Dreiecke SoSe 16
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Definition XIII.1: (Außenwinkel eines Dreiecks)
- Jeder Nebenwinkel zu einem Innenwinkel eines Dreiecks
 ist ein Außenwinkel zu diesem Dreieck.
ist ein Außenwinkel zu diesem Dreieck.
- Jeder Nebenwinkel zu einem Innenwinkel eines Dreiecks
Satz XIII.1: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 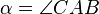 ,
, 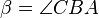 und
und 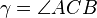 .
.
Es gilt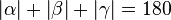 .
.
- Es sei
Beweis von Satz XIII.1 (Innenwinkelsatz für Dreiecke)
Übungsaufgabe
Satz XIII.2: (Starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der größen der beiden nicht anliegenden Innenwinkel dieses Dreiecks.
Beweis von Satz XIII.2: (Starker Außenwinkelsatz)
Übungsaufgabe
Aus dem starken Außenwinkelsatz folgt unmittelbar der schwache Außenwinkelsatz:
Satz XIII.3: (Schwacher Außenwinkelsatz)
- Das Maß eines jeden Außenwinkels
 eines Dreiecks ist jeweils größer als das Maß eines Innenwinkel von diesem Dreieck, sofern der Innenwinkel kein Nebenwinkel zum Außenwinkel
eines Dreiecks ist jeweils größer als das Maß eines Innenwinkel von diesem Dreieck, sofern der Innenwinkel kein Nebenwinkel zum Außenwinkel  des Dreiecks ist.
des Dreiecks ist.
- Das Maß eines jeden Außenwinkels

