Isomorphie und Homomorphie von Gruppen SoSe 2017
Aus Geometrie-Wiki
Isomorphie von GruppenBeispiele Deckdrehungen des Quadrates und
|
 |
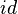 |
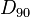 |
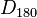 |
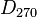
|
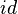 |
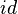 |
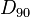 |
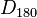 |
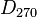
|
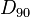 |
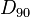 |
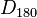 |
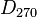 |
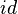
|
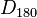 |
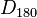 |
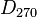 |
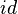 |
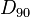
|
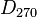 |
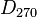 |
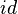 |
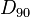 |
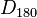
|
Tafel 2
 |
 |
 |
 |
|
 |
 |
 |
 |
|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
Beide Gruppentafeln weisen vom Prinzip her dieselbe Struktur auf:
Tafel 3
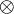 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
 |
 |
 |
 |

|
wobei sich folgender Zusammenhang ergibt:
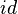 verhält sich in Tafel 1 wie
verhält sich in Tafel 1 wie  in Tafel 2 bzw. wie
in Tafel 2 bzw. wie  ind Tafel 3
ind Tafel 3
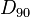 verhält sich in Tafel 1 wie
verhält sich in Tafel 1 wie  in Tafel 2 bzw. wie
in Tafel 2 bzw. wie  ind Tafel 3
ind Tafel 3
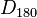 verhält sich in Tafel 1 wie
verhält sich in Tafel 1 wie  in Tafel 2 bzw. wie
in Tafel 2 bzw. wie  ind Tafel 3
ind Tafel 3
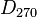 verhält sich in Tafel 1 wie
verhält sich in Tafel 1 wie 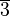 in Tafel 2 bzw. wie
in Tafel 2 bzw. wie  ind Tafel 3
ind Tafel 3
![\left[\mathbb{Z}, +\right]](/images/math/f/c/7/fc7fcef42998d302e2ccb2d198b4fc8d.png) und
und ![\left[2\mathbb{Z}, +\right]](/images/math/f/0/c/f0c30bf1ac80cd9a41480676290bea79.png)
Die Menge der ganzen Zahlen und die Menge der geraden ganzen Zahlen sind gleichmächtig zueinander: Die Abbildung  mit
mit 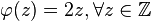 ordnet jeder ganzen Zahl genau eine gerade ganze Zahl zu. Umgekehrt bildet
ordnet jeder ganzen Zahl genau eine gerade ganze Zahl zu. Umgekehrt bildet 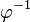 mit
mit 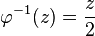 jeder geraden ganzen Zahl ihr Urbild bei
jeder geraden ganzen Zahl ihr Urbild bei  zu.
zu.  ist eine 1-1-Abbildung von der Menge der ganzen Zahlen auf die Mange der geraden ganzen Zahlen. 1-1-Abbildungen von-auf werden auch Bijektionen genannt.
ist eine 1-1-Abbildung von der Menge der ganzen Zahlen auf die Mange der geraden ganzen Zahlen. 1-1-Abbildungen von-auf werden auch Bijektionen genannt.
Beispiel 3
Alle Gruppen der Ordnung 3 sind isomorph zueinander.
Beweis: Übungsaufgabe
| * | e | a | b |
| e | e | a | b |
| a | a | b | e |
| b | b | e | a |
 |
 |
 |

|
 |
 |
 |

|
 |
 |
 |

|
 |
 |
 |

|
![[\mathbb{Z}_4,\oplus]](/images/math/8/0/9/809eadba6a0a17ba00b6356273a6aade.png)
![[D_4,\odot]](/images/math/1/4/e/14ec6becb43201b66ab330ca406d7d49.png) mit
mit 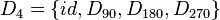 und
und 
