Klausurvorbereitung WS 12 13: Lisa reloaded oder der Heidelberger Viereckskreis

Was geschah mit Mayer2

Mayer2 wurde erst von seiner Frau verlassen, dann verließ er Deutschland. Bald wird er in der Doku-Soap "Deutschland deine Auswanderer" im Unterschichten-Fernsehen auf KOTZ als "Unser Mann in Kanada" zu sehen sein.

Lisa reloaded

Lisa, noch schöner und noch bezaubernder als im Sommersemester, bereitet sich auf Ihre Examensstunde (natürlich Geometrie) vor. Uwe ist Referendar im Fach Technik, sieht Lisas erste Unterrichtsentwürfe und baut ihr flugs den
Heidelberger Viereckskreis:

Klausurvorbereitung

1. Welches Thema wird Lisa wohl unterrichten?
2. Was hat das wohl mit unserer Klausur zu tun?
3. Wie wird es Uwe bzgl. Lisa ergehen?

Fragen über Fragen, die Sie sich in der besinnlichen Zeit schon mal stellen sollten.

Themenvorschläge für Lisa

Sätze am Kreis

1.) Es könnten Quadrate, Rechtecke, Dreiecke und gleichschenklige Trapeze gespannt werden. --Sissy66 08:40, 28. Dez. 2012 (CET) 2.) Man könnte ja für die Klausur zum Beispiel fragen: Beweisen Sie, dass jedes Quadrat ein Sehnenviereck ist. --Sissy66 08:44, 28. Dez. 2012 (CET)

Ein Drachenviereck ist nur dann ein Sehnenviereck, wenn die gleichen Winkel einen Rechten ergeben. --Sissy66 08:46, 28. Dez. 2012 (CET)

Sehnenviereck

Wie lautet der Satz im Sehnenviereck?

ein wenig Didaktik aus dem letzten Semester

--Oz44oz 23:22, 2. Jan. 2013 (CET)

Der Satz im Sehnenviereck :

Wenn ........ , dann...........

Wenn ein Viereck Sehnenviereck ist, dann sind die gegenüberliegenden Winkel supplementär.
Wenn die gegenüberliegenden Winkel in einem Viereck supplementär sind, dann ist das Viereck ein Sehnenviereck.
Ein Viereck ist genau dann Sehnenviereck, wenn seinen gegenüberliegenden Winkel supplementär sind.
--Yellow 14:04, 5. Jan. 2013 (CET)

Satz des Thales

Wenn Punkt C eines Dreiecks $\overline{ABC}$ auf dem Halbkreis über der Strecke $\overline{AB}$ liegt, dann ist $\overline{ABC}$ rechtwinklig am Punkt C.

ODER

Jeder Peripheriewinkel über dem Durchmesser eines Kreises ist ein Rechter. (Vorher muss natürlich Peripheriewinkel definiert werden)--Caro44 16:39, 6. Jan. 2013 (CET)

Definitionen

---

Definition Sehnenviereck

Ein Viereck, bei dem die Eckpunkte des Vierecks auf dem Umkreis dieses Vierecks liegen, ist ein Sehnenviereck. Die vier Seiten sind dann die Sehnen eines Kreises.

Definition Sehnendreieck

Schwachsinnig!! Jedes Dreieck ist ein "Sehnendreieck"!

Definition Umkreis eines Vierecks

Ein Umkreis eines Vierecks ist ein Kreis, der durch alle Eckpunkte des Vierecks geht.

Definition Peripheriewinkel

Wenn der Scheitelpunkt eines Winkels $\alpha$ auf einem Kreis k liegt und die beiden Schenkel von $\alpha$ k schneiden, dann heißt $\alpha$ Peripheriewinkel von k.

Was könnte man noch zum Heidelberger Viereckskreis definieren?--Caro44 17:00, 6. Jan. 2013 (CET)

Beweise

---

Der Heidelberger Viereckskreis stellt immer einen Umkreis dar.

Sätze, die etwas mit Umkreis zu tun haben:
- Sehnenvierecksatz
- Satz des Thales
- Zentri- Peripherie- Winkelsatz
- Peripheriewinkelsatz

Da der der Heidelberger Viereckskreis jedoch "Viereckskreis" heißt, fällt der Satz des Thales weg!--Caro44 17:16, 6. Jan. 2013 (CET)

Jedes Quadrat ist ein Sehnenviereck! (Idee von Sissi66)

--Caro44 16:57, 6. Jan. 2013 (CET)
@Caro44 Funktioniert so nicht. Der Satz über die gegenüberliegenden Winkel im Sehnenviereck sagt: Wenn Sehnenviereck, dann gegenüberliegende Winkel supplementär. Sie sagen weil gegenüberliegende Winkel supplementär, Quadrat ist Sehnenviereck. Sie brauchen also die Umkehrung des Satzes über die gegenüberliegenden Winkel im Sehnenviereck oder das Sehnenviereckskriterium. Für ein Quadrat ist es jedoch auch ganz leicht, unmittelbar zu zeigen, dass es einen Umkreis hat. Wie würden Sie diesen denn konstruieren? Diagonalenschnittpunkt und ich bin am Ziel ...--*m.g.* 19:35, 9. Feb. 2013 (CET)

Peripheriewinkelsatz

Jeder Peripheriewinkel über derselben Sehne ist gleich groß.

--Caro44 17:16, 6. Jan. 2013 (CET)

Satz A: In einem Sehnenviereck ist die Summe der gegenüberliegenden Winkel stets 180

Beweis 1	Beweis 2	Beweis 3

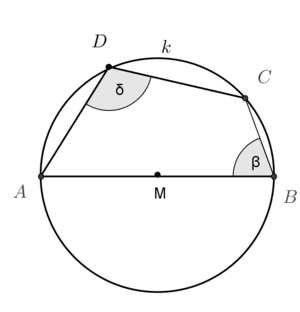Die Beweise sind noch zu führen. --Oz44oz 21:02, 7. Jan. 2013 (CET)

Fall 2

--jaegersasch

Fall 3

--jaegersasch

Sehr schön. Nun wird es aber günstig sein, den Satz über die gegenüberliegenden Winkel im Sehnenviereck vor dem Peripheriewinkelsatz zu beweisen. Könnten Sie auch ohne den Peripheriewinkelsatz auskommen? Tipp: M mit dazu nehmen und ein Fünfeck betrachten--*m.g.* 19:41, 9. Feb. 2013 (CET)

Fall 3.1

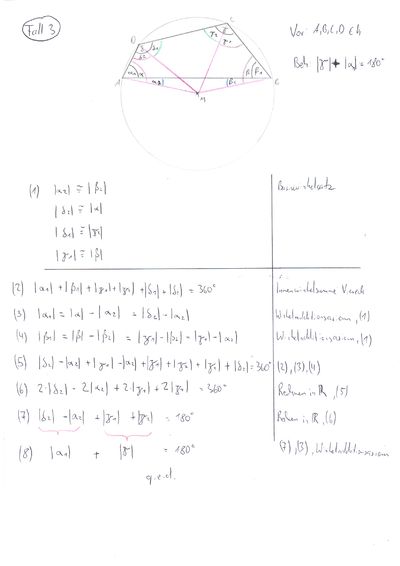
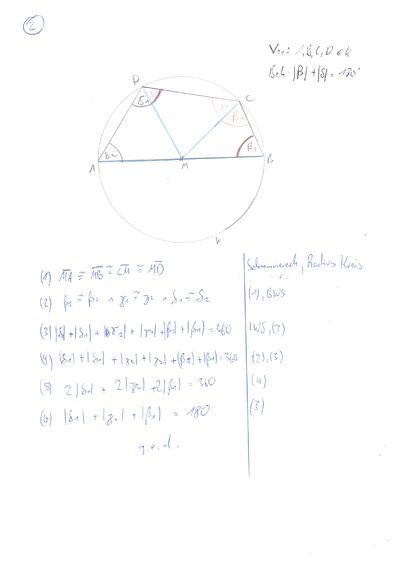
ergänzend kommt hinzu, dass die Strecken AM,BM,CM,DM natürlich Radius von k sind.

--jaegersasch

Tipp -*m.g.* 16:59, 20. Jan. 2013 (CET)

Lisa mag es symmetrisch.

Können wir davon ausgehen, dass bei einem gleichschenkligen Trapez die Symmetrieachse die Mittelsenkrechte der Strecke AB ist?--Aaliyah 14:49, 21. Jan. 2013 (CET)

Wir haben den Begriff der Symmetrie bzw. Symmetrieachse nicht definiert bzw. werden auch nicht mehr explizit tun. Trotzdem können Sie klären, wann ein Trapez symmetrisch ist, nämlich gerade dann, wenn es gleichschenklig ist.--*m.g.* 15:19, 21. Jan. 2013 (CET)

Vielleicht gefällt Lisa dieser Vorschlag! Satz: Jedes gleichschenklige Trapez ist ein Sehnenviereck. Und wegen der Achsensymmetrie gilt: 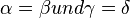$\alpha =\beta und \gamma = \delta$ .--Aaliyah 21:12, 21. Jan. 2013 (CET)

@ Aaliyahl. Könnte man dass nicht auch so formulieren: Trapez wo die nicht gegenüberliegenden Winkel kongruent zueinander sind? --Yellow 21:22, 21. Jan. 2013 (CET)

Klingt gut. Lisa könnte aber auch vorschlagen ein Trapez mit einem weiteren Paar kongruenter Seiten die nicht parallel sind außer es wäre ein Rechteck. Da hätte man dann Fallunterscheidungen zu zeigen, wohl eher kein Hit für die Klausur oder was meinen die Anderen? Welche Definitionen fallen euch noch ein?

--Yellow 21:23, 21. Jan. 2013 (CET)

@Yellow: Spricht man dann noch von einem Sehnenviereck, wenn man die benachbarten Winkel nimmt?--Aaliyah 22:19, 21. Jan. 2013 (CET)

Genau darum die Wahl mit nicht gegenüberliegend. Alpha ist kongruent zu beta. Delta wäre aber auch ein benachbarter Winkel zu alpha und ist nicht kongruent im gleichschenkligen Trapez. Wenn allerdings alpha, beta und delta kongruent sind, dann haben wir ein Rechteck und das wäre dann auch wieder ein Sehnenviereck. --Yellow 22:27, 21. Jan. 2013 (CET)

--Oz44oz 21:02, 21. Jan. 2013 (CET)

--Oz44oz 21:22, 21. Jan. 2013 (CET)

Wir haben uns überlegt: Ein Trapez ist ein Sehnenviereck, wenn seine beiden Diagonalen gleich lang sind.

Ein Trapez, das achensymmetrisch ist und das eine Symmetrieachse hat, die verschieden von den Diagonalen des Trapezes ist, heißt gleichschenkliges Trapez.

Dürften wir das so definieren?

oder könnten wir einfach sagen, dass die Mittelsenkrechte der Strecke AB die Symmetrieachse im gleichschenkligen Trapez ist ?

symmetrische Trapeze --*m.g.* 11:34, 23. Jan. 2013 (CET)

Die Begriffe Symmetrie, Symmetrieachse, Spiegelung etc. haben und werden wir im Rahmen der Einführung in die Geometrie nicht expizit definieren, so dass wir die Begriffe auch nicht verwenden können. Sie können den Begriff geleichschenkliges (symmetrisches) Trapez trotzdem in gewisser Weise mit Symmetriemitteln klären: Wir wissen de facto, dass die Mittelsenkrechte die Symmetrieachse einer Strecke ist. Jetzt schaun Sie sich mal die Lage aller Mittelsenkrechten eines beliebigen und eines gleichschenkligen Trapezes an.--*m.g.* 11:34, 23. Jan. 2013 (CET)

Sie sind zum Teil zu sehr entsprechend der Aufgabe aus dem Sommersemester auf die Diagonalen fixiert.

Im gleichschenkligen Trapez gilt:
Alle Punkte der Mittelsenkrechten der Strecke AB sind von den Punkten A und B gleichweit entfernt. Das gleiche gilt für die anderen drei Mittelsenkrechten?
Die Begründung liefert uns das Mittelsenkrechtenkriterium oder?

Außerdem können wir sagen, dass der Schnittpunkt aller Mittelsenkrechten der Umkreismittelpunkt ist oder müsste man das beweisen?

Das geht würde ich sagen. Und wir haben den Umkreis. Dann ist es doch mit den Radien ganz leicht zu beweisen, dass der Schnittpunkt der Mittelsenkrechten der Kreismittelpunkt ist. --Yellow 15:21, 23. Jan. 2013 (CET)

Ich bin mir nicht sicher, dass wir schon von dem Umkreis reden können. Das wollen wir doch beweisen? Wir wissen aber, dass der Schnittpunkt aller Mittelsenkrechten im Dreieck auf alle Fälle einen Umkreis hat.

Zwei der Mittelsenkrechten im gleichschenkligen Trapez fallen aufeinander, da zwei Seiten parallel zueinander sind und bilden eine gemeinsame Mittelsenkrechte. Hilft uns das weiter?
<br /

Wenn ich gezeigt habe das für Schnittpunkt P gilt |PA|=|PB|=|PC|=|PD| dann ist , das doch der Radius, und alle Punkte liegen somit auf k. Den Umkreis würde ich eher mit Widerspruch beweisen. Punkt D ist nicht Element von k.
Parallel sagt nicht aus, dass die Seiten sich im gleichen Verhältnis schneiden.
--Yellow 15:50, 23. Jan. 2013 (CET)

--Oz44oz 21:07, 23. Jan. 2013 (CET)
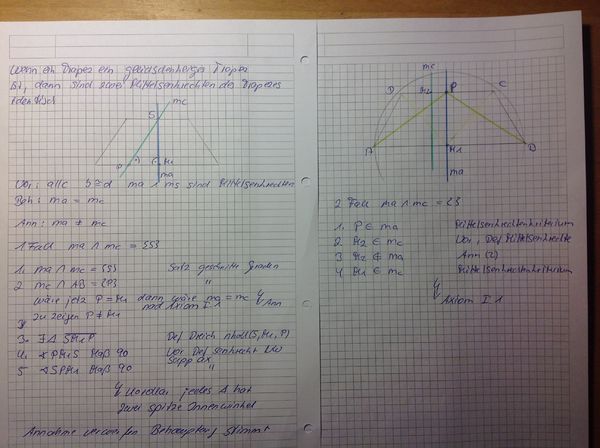
dann könnten wir doch sicherlich eine neue Definition aufstellen, die dann heißt: Ein gleichschenkligses Trapez ist ein viereck, bei dem zwei gegenüberliegende Seiten eine identische mittelsenkrechte besitzen.

Gilt aber nur für das Seitenpaar welches parallel ist. Die Mittelsenkrechten der Schenkel sind nicht identisch, außer Viereck wäre Quadrat oder Rechteck. --Yellow 14:10, 25. Jan. 2013 (CET)

Beweis zum Gleichschenkligen Trapez

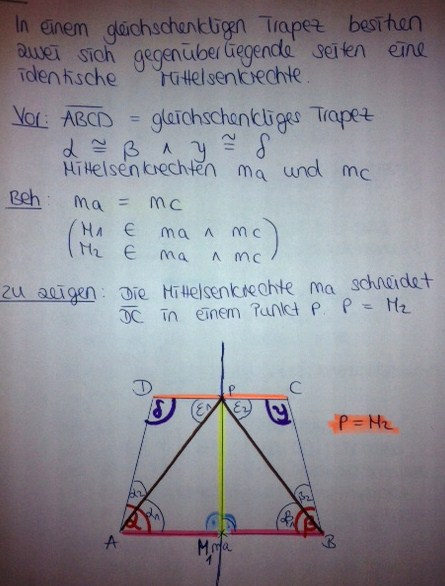
Wir haben ja nun herausgefunden, dass bei einem gleichschenkligen Trapez zwei sich gegenüberliegende Mittelsenkrechten zusammenfallen bzw. identisch sind. Dies könnte man nun beweisen!

Skizze:

Beweis:

--Caro44 15:01, 3. Feb. 2013 (CET)
Wo ist bei dir in der Skizze M2 ? (Sallyfield)

P ist M2! M2 ist der Mittelpunkt der Strecke CD!Ich nehme zuerst an, dass die Mittelsenkrechte von AB die Strecke CD in dem Punkt P schneidet! Mein Ziel ist es dann darauf zu kommen, dass M2 und P identisch sind und somit die Mittelsenkrechte von AB durch den Mittelpunkt (M2) von CD geht.--Caro44 15:17, 3. Feb. 2013 (CET)

bei Fall 2 bin ich mir nicht sicher ob dass so geht. --Yellow 22:24, 4. Feb. 2013 (CET)
Kann man wenn man ein gleichschenkliges Trapez im Viereckskreis spannt, schon sagen, dass die nicht gegenüberliegenden Innenwinkel, kongruent zueinander sind?--SallyField 19:36, 6. Feb. 2013 (CET)