Konstruktion eines Sehnen-Tangenten-Viereck
Wir haben uns heute (lang) Gedanken um das Sehnen-Tangenten-Viereck gemacht. Das ein Quadrat ein Repräsentant ist für diesen Begriff ist uns völlig bewusst. Demnach haben wir die Winkelhalbierenden betrachtet und auch die Mittelsenkrechten, die sich dort in einem Punkt schneiden. Wir erachteten dies kurzzeitig als ein Kriterium dafür, dass ein Viereck ein STV ist. Kurz darauf kamen wir zu dem Entschluss, dass genau dann, wenn sich diese beiden Transversalen in einem Punkt schneiden AUSSCHLIEßLICH ein Quadrat als STV entstehen kann - da es aber auch noch andere Repräsentanten geben musste brachte uns das nicht weiter.
Nach längerer Diskussion über andere Herangehensweisen haben wir aufgehört uns Gedanken darüber zu machen. Nach einem kurzen Gespräch mit einer Tutorin bin ich auf den Gedanken gekommen, die gesamte Sache anders herum aufzuziehen, nämlich so, dass wir für das Endergebnis zwei Kreise brauchen, nämlich einen großen und einen kleineren, der im inneren des großen ist.
Geogebra bietet ja nun ganz elegant die Möglichkeit, hier etwas herumzuprobieren und die Tangentenschnittpunkte an den kleinen Kreis konnte man einfach mit dem Thaleskreis erzeugen. Die letzte Tangente stellte sich jedoch als problematisch heraus. Hier jedoch half Geogebra und man konnte ziehen und drehen wie man lustig war.
FRAGE: Ist es wirklich so kompliziert, dass ein STV nur (und nur dann) entsteht, wenn das Verhältnis zwischen dem äußerem Kreis und dem inneren Kreis so gestimmt ist, dass der äußere 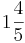 mal so groß ist, wie der kleinere, innere Kreis? Wenn die Proportionen so gelegt sind, dann funktioniert es auf jeden Fall.
mal so groß ist, wie der kleinere, innere Kreis? Wenn die Proportionen so gelegt sind, dann funktioniert es auf jeden Fall.
Eine Antwort dazu - siehe Unten!--Tutorin Anne 22:21, 14. Jul. 2011 (CEST)
Ich denke es müsste einfacher gehen. Damit aber der Kompliziertheit nicht genug. Der Mittelpunkt des äußeren Kreises darf nicht irgendwo liegen. Er muss auf einem Kreis liegen, dessen Mittelpunkt gleichzeitig der Mittelpunkt des kleinen Kreises ist und dessen Radius 5,5 mal kleiner ist als der Radius des kleinen Kreises. D. h. der Abstand zwischen dem Mittelpunkt des kleinen Kreises zum Mittelpunkt des großen Kreises muss exakt der Radius des kleinen Kreises : 5,5 sein!
Das Quadrat scheint hier übrigens eine Ausnahme zu sein?!
Hier eine Skizze - probiert es aus und sagt mir wenn es nach dieser (doch sehr ausführlichen) operativ-genentischen Anweisung (Definition würde ich es nicht nennen) nicht funktioniert. Ich denke es funktioniert IMMER.
Vllt. kann auch ein Dozent hierzu etwas anfügen, weil es ist halt schon irgendwie kompliziert und ich bin mir sicher, dass es einfacher auch gehen MUSS - vllt. denke ich aber auch zu kompliziert. --Flo60 00:32, 14. Jul. 2011 (CEST)
Danke für den interessanten, ausführlichen Beitrag.
Also deiner Geogebra-Applikation, sieht es so weit ganz gut aus. Aber wie bist du denn auf diesen Spezialfall, diese Verhältnisse gekommen? Wie kannst du die Richtigkeit begründen?
Zur Frage: Hier ein Gegenbeispiel: Bewege die Punkte und du kannst noch weitere Gegenbeispiele erhalten!

