Kontrapostionen SoSe 2018
Bilden der KontrapositionImplikation
Umkehrung
Kontraposition
HandlungsanleitungBilde die Umkehrung der Implikation. Negiere Voraussetzung und Behauptung einzeln in dieser Umkehrung. BeispieleHöhensatzImplikationWenn ein Dreieck rechtwinklig ist, dann hat das Quadrat über der Höhe dieses Dreiecks denselben Flächeninhalt wie das Rechteck, das aus den beiden Hypotenusenabschnitten gebildet werden kann. UmkehrungWenn das Quadrat über der Höhe auf die längste Seite eines Dreiecks so groß wie das Produkt der Längen der beiden Teilstrecken ist, in die der Höhenfußpunkt die größte Seite des des Dreiecks teilt, dann ist das Dreieck rechtwinklig. KontrapositionWenn das Quadrat über der Höhe auf die längste Seite eines Dreiecks nicht so groß wie das Produkt der Längen der beiden Teilstrecken ist, in die der Höhenfußpunkt die größte Seite des des Dreiecks teilt, dann ist das Dreieck nicht rechtwinklig. BasiswinkelsatzKontrapositionWenn ein Dreieck keine gleichgroßen Winkel hat, dann ist es auch nicht gleichschenklig. Innenwinkelsatz für DreieckeKontrapositionWenn ein Vieleck nicht die die Innenwinkelsumme Schnittpunkte von GeradenImplikationWenn zwei Geraden nicht identisch sind, dann haben sie nicht mehr als einen Punkt gemeinsam. UmkehrungWenn zwei Geraden nicht mehr als einen Punkt gemeinsam haben, dann sind sie auch nicht identisch. KontrapositionWenn zwei Geraden zwei Punkte gemeinsam haben, dann sind sie identisch. Wozu die Kontraposition?Die Kontraposition hat immer denselben Wahrheitswert wie die zugehörige Implikation. anstelle der Implikation können wir also auch die Kontraposition beweisen. Das Ganze im Video[ www.youtube.com is not an authorized iframe site ] |

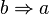
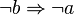
 hat, dann ist es kein Dreieck.
hat, dann ist es kein Dreieck.

