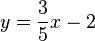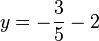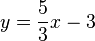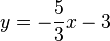|
Einstiegsaufgaben
Koordinatensysteme und Koordinaten sind Ihnen aus der Schule bekannt. Hier ein paar Aufgaben zur Auffrischung.
Aufgabe 1
Hier sehen Sie eine Applikation, die mittels Geogebra generiert wurde. Geogebra stellt uns ein Koordinatensystem zur Verfügung, auf desssen Grundlage wir Punkte und andere Objekte mittels ihrer Koordinaten darstellen können. In die Applikation wurde bereits der Punkt  eingetragen. Er hat die Koordinaten eingetragen. Er hat die Koordinaten 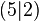 . Nehmen wir an, dass nun auch der Punkt . Nehmen wir an, dass nun auch der Punkt 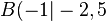 in der Applikation dargestellt werden soll. Hierzu geben wir in die Befahlszeile am unteren Rand der Applikation die Zeichenfolge B=(-1,-2.5) ein, schließen mit der Eingabetaste ab und der Punkt in der Applikation dargestellt werden soll. Hierzu geben wir in die Befahlszeile am unteren Rand der Applikation die Zeichenfolge B=(-1,-2.5) ein, schließen mit der Eingabetaste ab und der Punkt  wird entsprechend angezeigt. wird entsprechend angezeigt.
- Generieren Sie in obiger Applikation die Punkte
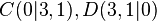
- Die Geogebra-Syntax zur Berechnung der Wurzel aus 2 lautet sqrt(2). Lassen Sie in der obigen Applikation den Punkt
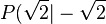 generieren. generieren.
- Verbinden Sie die Punkte
 zu einem Dreieck mittels des Befehls vieleck[A,B,C]. zu einem Dreieck mittels des Befehls vieleck[A,B,C].
- Lassen Sie den Schwerpunkt
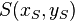 des Dreiecks des Dreiecks  einzeichnen. Die Koordinate einzeichnen. Die Koordinate 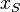 ist der Mittelwert der x-Koordinaten der Punkte ist der Mittelwert der x-Koordinaten der Punkte  . Analog gilt für Fehler beim Parsen(Syntaxfehler): y_S=\frac{y_A+y_B+y_C}{3 . Analog gilt für Fehler beim Parsen(Syntaxfehler): y_S=\frac{y_A+y_B+y_C}{3
.
Aufgabe 2
Viele Geraden lassen sich bekannterweise durch Gleichungen der Form 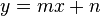 darstellen. darstellen.  und und  sind dabei beliebige aber feste reelle Zahlen. sind dabei beliebige aber feste reelle Zahlen. 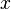 und und 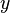 sind reelle Zahlen, die als geordnetes Paare sind reelle Zahlen, die als geordnetes Paare 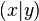 , die Punkte beschreiben, die zur jeweiligen Geraden gehören. , die Punkte beschreiben, die zur jeweiligen Geraden gehören.
Darstellungen von Geraden können mittels Geogebra generiert werden, indem man die Geradengleichung in die Eigabezeile einträgt.
Lassen Sie die Geraden in der obigen Geogebraapplikation darstellen, die durch die folgenden Gleichungen beschrieben werden.
-
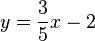
-
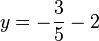
-
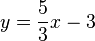
-
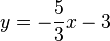
Analytische Geometrie?
In der analytischen Geometrie werden geometrische Objekte mittels Koordinaten, Gleichungen und Relationen beschrieben.
Als Begründer der Koordinatengeometrie gelten René Descartes (1596 - 1650) und Pierre de Fermat (1607 - 1665). Ihre Idee besteht darin, rechnerische und algebraische Methoden auf die Geometrie anzuwenden.
In der Vorlesungsreihe werden wir sehen, dass viele geometrische Objekte und Relationen sich mittels der Koordinatenmethode beschreiben lassen. Gleichzeitig werden Grenzen der Koordinatenmethode aufgezeigt und später mittels der Vektorrechnung überwunden.
|  eingetragen. Er hat die Koordinaten
eingetragen. Er hat die Koordinaten 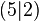 . Nehmen wir an, dass nun auch der Punkt
. Nehmen wir an, dass nun auch der Punkt 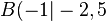 in der Applikation dargestellt werden soll. Hierzu geben wir in die Befahlszeile am unteren Rand der Applikation die Zeichenfolge B=(-1,-2.5) ein, schließen mit der Eingabetaste ab und der Punkt
in der Applikation dargestellt werden soll. Hierzu geben wir in die Befahlszeile am unteren Rand der Applikation die Zeichenfolge B=(-1,-2.5) ein, schließen mit der Eingabetaste ab und der Punkt  wird entsprechend angezeigt.
wird entsprechend angezeigt.
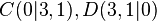
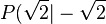 generieren.
generieren.
 zu einem Dreieck mittels des Befehls vieleck[A,B,C].
zu einem Dreieck mittels des Befehls vieleck[A,B,C].
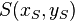 des Dreiecks
des Dreiecks  einzeichnen. Die Koordinate
einzeichnen. Die Koordinate 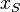 ist der Mittelwert der x-Koordinaten der Punkte
ist der Mittelwert der x-Koordinaten der Punkte 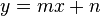 darstellen.
darstellen.  und
und  sind dabei beliebige aber feste reelle Zahlen.
sind dabei beliebige aber feste reelle Zahlen. 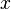 und
und 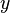 sind reelle Zahlen, die als geordnetes Paare
sind reelle Zahlen, die als geordnetes Paare 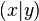 , die Punkte beschreiben, die zur jeweiligen Geraden gehören.
, die Punkte beschreiben, die zur jeweiligen Geraden gehören.