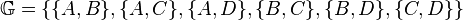Lösung Aufgabe 4.01 SoSe 2018
Aus Geometrie-Wiki
Aufgabe 4.01 SoSe 2018Wir betrachten das folgende Modell
Lösung 11. Da das Modell
Modellpunkte Modellgeraden Inzidenz Lösung 2Lösung 3 |
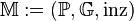 für die Inzidenzgeometrie:
für die Inzidenzgeometrie: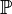 :
: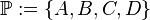
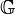 :
: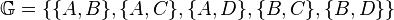
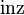 :
: inzidiert mit einer Geraden
inzidiert mit einer Geraden  , wenn er zu
, wenn er zu 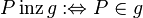
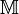 kein Modell für die ebene Inzidenzgeometrie?
kein Modell für die ebene Inzidenzgeometrie?