Lösung von Aufg. 13.6 (WS 11/12)
Aus Geometrie-Wiki
Beweisen Sie den Innenwinkelsatz für Dreieckehttp://upload.wikimedia.org/wikipedia/commons/8/8f/Button_poeme.png
Gegeben sei ein Dreieck ABC. (nach schulüblichen Bezeichnungen) Die Winkel 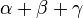 =180.
=180.
Vor: Dreieck ABC
Beh: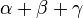 =180
=180
Bew:
| Beweisschritt | Begründung |
|---|---|
1)  g: g: 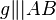  C C  g g
|
Existenz Parallele, Parallelenaxiom |
2)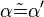
|
Wechselwinkelsatz |
3)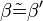
|
Wechselwinkelsatz |
4)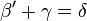
|
Axiom IV.3 |
5)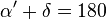
|
Nebenwinkel, Axiom IV.4 |
6)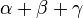 =180 =180
|
(2),(3),(4),(5) |
| q.e.d. |
--Adores 00:46, 26. Jan. 2012 (CET)

