Lösung von Aufg. 14.1 (SoSe 11)
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parallel zu
geht und parallel zu  ist.
ist.
Voraussetzung: Gerade g 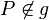 Behauptung: Es existiert eine Gerade h durch P, die parallel zu g ist.
Behauptung: Es existiert eine Gerade h durch P, die parallel zu g ist.
Beweisführung in der absoluten Geometrie:
--Flo60 23:11, 12. Jul. 2011 (CEST)
| 1 | Sei P ein Punkt in  |
Definiton Halbebene |
| 2 | 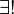 Strahl in Strahl in  für den gilt, dass er durch P verläuft und auf g senkrecht steht. Sei dieser für den gilt, dass er durch P verläuft und auf g senkrecht steht. Sei dieser 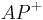 |
Existenz und Eindeutigkeit einer Senkrechten auf einer Geraden, Axiom vom Lineal, Abstandsaxiom, (1) |
| 3 | senkrecht = Winkelmaß 90 | Definition Senkrechte von Geraden |
| 4 | Wenn die Stufenwinkel an geschnittenen Geraden kongruent zueinander sind, dann sind die Geraden |
Umkehrung Stufenwinkelsatz |
| 5 | 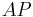 teilt die Ebene in zwei Halbebenen ein teilt die Ebene in zwei Halbebenen ein |
Def. Halbebene, (2) |
| 6 | In jeder Halbeneben bzgl. 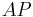 existiert an P genau ein Strahl mit dem Maß 90 existiert an P genau ein Strahl mit dem Maß 90 |
Winkelkonstruktionsaxiom, (5) |
| 7 | Durch die in 6 erzeugten Strahlen exisiert eine eindeutige Gerade h | Axiom I.1 und Axiom I.2, (6) |
| 8 | Da der Winkel 90 gleich ein rechter ist und dieser nach Def. kongruent zu seinen Nebenwinkeln ist, sind die Stufenwinkel kongruent zueinander und die Geraden h und g sind parallel | (3), (4), (7) |
Leider zeigt mir dieser Beweis nicht die Eindeutigkeit, da ich nur durch den Stufenwinkelsatz (und nicht deren Umkehrung) ein Kriterium zur Definition von PArallelen schaffen kann. Den kriege ich aber nur durch das Parallelenaxiom. Das kann man sich so Vorstellen wie bei Microsoft. Die Programme sind da auch immer rückgekoppelt, damit man ja ein update kaufen muss :-) --Flo60 23:06, 12. Jul. 2011 (CEST)
wunderbare Erkenntnis - genau so ist es!--Schnirch 13:36, 19. Jul. 2011 (CEST)
Das Problem bei diesem Beweis (meiner Meinung nach) ist Schritt 2. Man kann mit dem Winkelkonstruktionsaxiom nicht einfach eine Lotgerade durch einen Punkt konstruieren. Also muss man entweder mit der Exisitenz und Eindeutigkeit der Lotgerade diese konstruieren (also die Begründung ändern) oder aber,man trägt irgend einen Strahl an, dessen Maß man anschließend misst und an diesen Strahl GP+ trägt man anschließend wieder einen Strahl PC+ mit dem selben Maß, so dass ein paarallele Gerade erzeugt wird.
(siehe Applikation:)--Tutorin Anne 17:12, 19. Jul. 2011 (CEST)
Die Frage, die sich mir stellt, dürfen wir das EP in dieser Übung bereits verwenden? Dieser Satz steht noch vor dem EP, im Skript. Falls man das EP benutzen darf, welche Sätze darf man nach dem EP noch benutzen? Danke.--Teufelchen 20:35, 16. Jul. 2011 (CEST)
Wenn du dir die Formulierung des Satzes anschaust, dann lässt sich daraus ableiten, dass nur die Existenz gezeigt werden soll. Dafür wird das EP nicht benötigt und sollte deshalb nicht genutzt werden. Wie müsst der Satz lauten, damit auch die Eindeutigkeit gezeigt werden müsste?
In der euklidischen Geometrie (also mit Euklidischem Parallelenaxiom) gelten auch alle Sätze aus der absoluten Geometrie.--Tutorin Anne 17:12, 19. Jul. 2011 (CEST)

