Lösung von Aufg. 14.6 (SoSe 11)
Aus Geometrie-Wiki
Man beweise: Ein Punkt  gehört genau dann zur Winkelhalbierenden des Winkels
gehört genau dann zur Winkelhalbierenden des Winkels  , wenn er zu den Schenkeln von
, wenn er zu den Schenkeln von  jeweils denselben Abstand hat.
jeweils denselben Abstand hat.
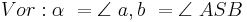
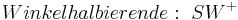
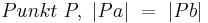
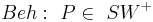
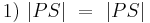 ....(trivial)
....(trivial)
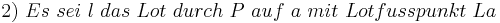 ....(Ex. + Eind. des Lots)
....(Ex. + Eind. des Lots)
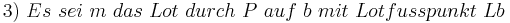 ....(Ex. + Eind. des Lots)
....(Ex. + Eind. des Lots)
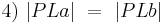 ....(Vor.)
....(Vor.)
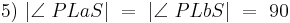 ....(Def. Lot, Vor)
....(Def. Lot, Vor)
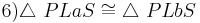 ....(1,4,5, SsW, Der gilt, nach Korollar1 zum schwachen Außenwinkelsatz haben die Dreiecke mindestens zwei spitze Innenwinkel, Damit liegt dem rechten Winkel die längste Seite gegenüber (Satz größerer Winkel, größere Seite))
....(1,4,5, SsW, Der gilt, nach Korollar1 zum schwachen Außenwinkelsatz haben die Dreiecke mindestens zwei spitze Innenwinkel, Damit liegt dem rechten Winkel die längste Seite gegenüber (Satz größerer Winkel, größere Seite))
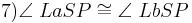 ....(6)
....(6)
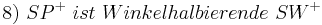 ....(7, Def WH)
....(7, Def WH)
q.e.d. ---phil- 22:19, 19. Jul. 2011 (CEST)

