Lösung von Aufg. 6.2P (WS 18 19)
Aus Geometrie-Wiki
Definieren Sie den Begriff: "konvexe Punktmenge" indem Sie die verbal formulierte Definition (siehe Wiki-Skript) in eine geeignete "Mengenschreibweise" übersetzen.
M ist konvex, wenn gilt: ...
Strecke AB vereinigt mit M ist ungleich der leeren Menge
sobald M ein Element besitzt, ist diese Vereinigung immer ungleich der leeren Menge, das kann also nicht stimmen. Weitere Ideen?--Schnirch (Diskussion) 12:13, 21. Nov. 2018 (CET)
Es existiert ein Punkt A und ein Punkt B Element M für das gilt: Strecke AB Element M --Student01 (Diskussion) 16:10, 21. Nov. 2018 (CET)
nun, nur weil eine solche Streckeexistiert, gilt das ja noch lange nicht für alle möglichen Punkte aus M, oder?--Schnirch (Diskussion) 12:04, 29. Nov. 2018 (CET)
M ist konvex <=> M={A,B} 
 ⊂ M. Alternativ: M={A,B |
⊂ M. Alternativ: M={A,B |  ⊂ M}--CIG UA (Diskussion) 12:38, 23. Nov. 2018 (CET)
⊂ M}--CIG UA (Diskussion) 12:38, 23. Nov. 2018 (CET)
auch hier fehlt mir noch die Allaussage--Schnirch (Diskussion) 12:04, 29. Nov. 2018 (CET)
Man könnte M noch {C} hinzufügen und sich auf die Symmertrie der Relation beziehen, also: M={A,B,C | 

 (und damit auch
(und damit auch  ⊂ M}.--CIG UA (Diskussion) 10:55, 30. Nov. 2018 (CET)
⊂ M}.--CIG UA (Diskussion) 10:55, 30. Nov. 2018 (CET)
beginnen Sie mal so:...--Schnirch (Diskussion) 13:06, 3. Dez. 2018 (CET)
M ist konvex, wenn 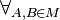 :
: 
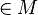 --Azalea (Diskussion) 14:50, 5. Feb. 2019 (CET)
--Azalea (Diskussion) 14:50, 5. Feb. 2019 (CET)

