Lösung von Aufg. 7

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

$\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace$

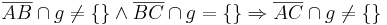
Lösung--Schnirch 12:33, 22. Dez. 2010 (UTC)

Vor.:

• drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E
• $\ g \subset E$
• $\ A,B,C \notin g$
• $\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace$
  

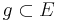
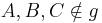
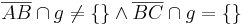
Beh.: 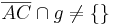$\overline{AC} \cap g \neq \lbrace \rbrace$

Der folgende Beweis ist nur einer von vielen möglichen. Fühlen Sie sich frei Ihre Version auch mit hier einzustellen!
Die Idee des folgenden Beweises liegt darin, sich einen weiteren Punkt P in der Halbebene 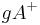$\ gA^{+}$ zu erzeugen, der nichtkollinear zu A,B,C ist und dann das Axiom von Pasch mehrfach anzuwenden:

Beweis

Nr.	Beweisschritt	Begründung
(I)	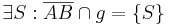$\exists S: \overline{AB} \cap g = \lbrace S \rbrace$	Vor.
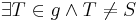
(II)	$\exists T \in g \wedge T \not= S$	Axiom I/2
(III)	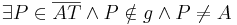$\exists P \in \overline{AT} \wedge P \notin g \wedge P \not=A$	Axiom vom Lineal
(IV)	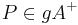$\ P \in gA^{+}$	(II), (III)
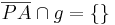
(V)	$\overline{PA} \cap g = \lbrace \rbrace$	(IV), Def. Halbebene
(VI)	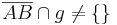$\overline{AB} \cap g \not= \lbrace \rbrace$	Vor.
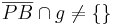
(VII)	$\overline{PB} \cap g \not= \lbrace \rbrace$	(V), (VI), Axiom von Pasch
(VIII)	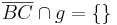$\overline{BC} \cap g = \lbrace \rbrace$	Vor.
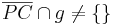
(IX)	$\overline{PC} \cap g \not= \lbrace \rbrace$	(VII), (VIII), Axiom von Pasch
(X)	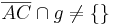$\overline{AC} \cap g \not= \lbrace \rbrace$	(V), (IX), Axiom von Pasch