Lösung von Aufg. 7.3P (WS 13/14)

Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:

$\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace\Rightarrow \overline{AC}\cap g=\lbrace \rbrace$

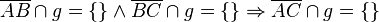
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 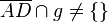$\overline{AD}\cap g\not=\lbrace \rbrace$ und nutzen Sie den Satz von Pasch)

Verstehe nicht wirklich warum wir noch den vierten Punkt D brauchen. Man kann auch ohne den zusätzlichen Punkt zeigen, dass die Behauptung stimmt.

Voraussetzung: 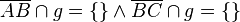$\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace \$

Behauptung: 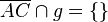$\overline{AC}\cap g=\lbrace \rbrace$
Annahme: 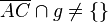$\overline{AC}\cap g\not=\lbrace \rbrace$

Nr.	Schritt	Begründung
1.	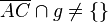$\overline{AC}\cap g\not=\lbrace \rbrace$	Annahme
3.	Wenn die Gerade g eine Seite schneidet, dann schneidet sie genau eine weitere Seite des Dreiecks. Gerade g schneidet entweder $\overline{AB}$ oder $\overline{BC}$	Satz von Pasch
4.	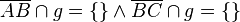$\overline{AB}\cap g=\lbrace \rbrace \wedge \overline{BC}\cap g=\lbrace \rbrace \$	Voraussetzung
5.	Die Annahme ist zu verwerfen, die Behauptung stimmt.	3),4)

--Picksel (Diskussion) 11:05, 18. Jun. 2014 (CEST)

Der Beweis ist so nicht möglich, da du in Schritt 3 den Satz von Pasch anwendest. Dieser gilt aber nur bei Dreiecken. A, B und C sind aber kollinear.--Tutorin Anne (Diskussion) 09:06, 1. Jul. 2014 (CEST)