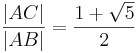Lösung von Aufg. 8.3

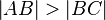Der Punkt $\ B$ möge die Strecke $\overline{AC}$ derart in die Teilstrecken $\overline{AB}$ und $\overline{BC}$ teilen, dass $\left| AB \right| > \left| BC \right|$ gilt. Beweisen Sie:
Wenn 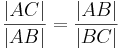$\frac{ \left| AC \right| }{\left| AB \right| } = \frac{\left| AB \right| }{\left| BC \right| }$, dann $\frac{ \left| AC \right| }{\left| AB \right|} = \frac{1 + \sqrt{5}}{2}$.

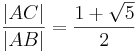Die nachfolgende super korrekte und ausführliche Lösung wurde von einer Studentin ins Netz gestellt:--Schnirch 14:08, 14. Dez. 2010 (UTC)

Voraussetzung:

1) $\frac{|AC|}{|AB|} = \frac{|AB|}{|BC|}$

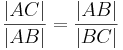
2) $\ |AB| + |BC| = |AC|$

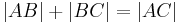
Behauptung:

$\frac{|AC|}{|AB|} = \frac{1 + \sqrt{5}}{2}$

Beweis:

(2) $\ |AB| + |BC| = |AC|$

$\Rightarrow \ \ |BC| = |AC| - |AB|$

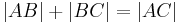
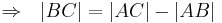
eingesetzt in (1) folgt daraus

$\frac{|AC|}{|AB|} = \frac{|AB|}{|AC| - |AB|} \ \ \ \ \ | \ \cdot |AB| \cdot(|AC| - |AB|)$

$\Rightarrow \ \ |AC| \cdot (|AC| - |AB|) = |AB|^2 \ \ \ \ \ | \ -|AB|^2$

$\Rightarrow \ \ |AC|^2 - |AB| \cdot |AC| - |AB|^2 = 0$

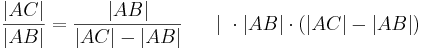
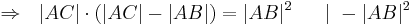
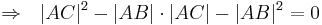
Mit der p,q-Formel folgt daraus

$|AC|_{1/2} = \frac{|AB|}{2} \pm \sqrt{\frac{|AB|^2}{4} + |AB|^2}$

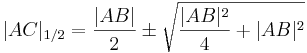
Die 2. Lösung mit negativem Vorzeichen fällt weg.

$\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \sqrt{ \frac{5 \cdot |AB|^2}{4} }$

$\Rightarrow \ \ |AC| = \frac{|AB|}{2} + \frac{|AB|}{2} \cdot \sqrt{5}$

$\Rightarrow \ \ |AC| = \frac{|AB|}{2} \cdot ( 1 + \sqrt{5})$

$\Rightarrow \ \ |AC| = |AB| \cdot \frac{ 1 + \sqrt{5} }{2} \ \ \ \ \ | \ : |AB|$

$\Rightarrow \ \ \frac{|AC|}{|AB|} = \frac{ 1 + \sqrt{5} }{2}$

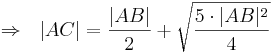
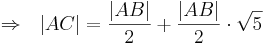
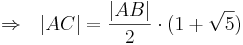
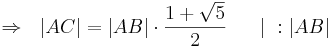
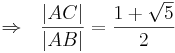
q.e.d --Sternchen 17:05, 10. Jun. 2010 (UTC)