Lösung von Aufg. 9.3 (SoSe 11)
Definieren Sie noch einmal die Begriffe Halbgerade 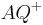 und
und 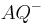 . In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.5 äquivalent sind.
. In diesen neuen Definitionen dürfen Sie die Zwischenrelation nicht explizit verwenden. Beweisen Sie dann, dass Ihre neuen Definitionen zur | Definition II.5 äquivalent sind.
Wie die neue Definition heißt, haben wir in der Übung bespochen. Aus Zeitgründen dann jedoch die Auflösung des Beweises der Äquivalenz auf einen anderen Termin verschoben (durchaus verständlich). Ich möchte mich hier mal versuchen und eine Beweismöglichkeit darstellen. Vllt. kann ja der eine und der ander und die eine und die andere seinen/ihren Senf dazugeben.
Defininition 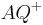 nach II.5 (im folgenden als DefA für Definition alt):
nach II.5 (im folgenden als DefA für Definition alt): 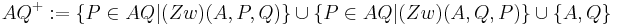
Defininition 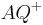 neu (im folgenden als DefN für Definition neu):
neu (im folgenden als DefN für Definition neu): 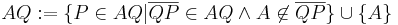
Beweis über zwei Schritte: Schritt 1: "=>" Schritt 2: "<="
Es sei aufgrund der einfacheren Bearbeitung (man spart sich einen ganzen Beweisschritt) folgender Fall vorweggeschickt, der für bei Seiten gilt, wegen der Reflexivität der "="-Relation:
Voraussetzung: 
Behauptung: 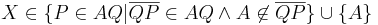
Fall 1: X = A => Da A in beiden Fällen als einzelne Menge vereinigt wird ist dieser Fall trivial.
Fall 2 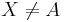
Beweis "=>"
| 1 | Es gilt: koll(A, Q, X) | Voraussetzung, Zwischenrelationdefinition |
| 2 | 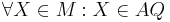 |
Axiom I.2, (1) |
| 3 | AX| + |XQ| = |AQ| => 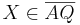 \ \ 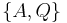 |
Def. Zwischenrelation, Voraussetzung |
| 4 | AQ| + |QX| = |AX| => 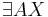 |
Def. Zwischenrelation, Voraussetzung |
| 5 | 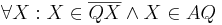 |
(1), (2), (3), (4) |
| 6 | wg. X  A: A: 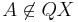 |
(5) |
| 7 | 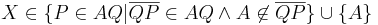 |
(6) |
Irgendwie schaut das noch wie ein riesengroßes gewurschtel aus und sicher bin ich mir keineswegs.
In Beweisschritt 2 schauts da allerdings etwas anders aus:
Beweis: "<="
| 1 | 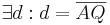 |
Axiom III.1, Vor. |
| 2 | 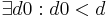 |
Rechnen in R, (1) |
| 3 | 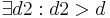 |
Rechnen in R, (1) |
| 4 | 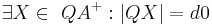 |
Axiom vom Lineal, (2) |
| 5 | Zw(A, X, Q) | (4), Hilfssatz I |
| 6 | Sei Z ein Punkt der Geraden AQ für den gilt: Zw(A, Q, Z) 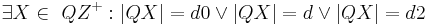 |
Axiom vom Lineal, (1), (2), (3) |
| 7 | AQ| + |QX| = |AX| => Zw(A, Q, X) | (6), Def. Zwischenrelation |
| 8 | Für d0=0 gilt: X = Q und für d(QZ) = d(QX) gilt: Z  X X |
Axiom II.1, (2), (6) Anmerkung: ich konnte nicht in Abstandsschreibweise schreiben weil das wiki meint es müsste das vorherige dann rausstreichen |
| 9 | Für 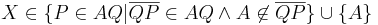 gilt: gilt: 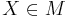 |
(5), (7), (8) |
Punkt Z wird aus dem Axiom vom Lineal generiert, das habe ich aber nicht mehr extra hingeschrieben, das ist trivial, denke ich.
Hilfssatz I: Für |QX| = d0 gilt für QA^{+}: Zw(A, X, Q)
Annahme: Zw(X, A, Q)
| a | XA| + |AQ| = |XQ| | Annahme |
| b | XA| + d = d0 | (a), (1), (4) |
| c | Annahme ist zu verwerfen wg. Nichtlösbarkeit der Aufgabe | (b) |
--Flo60 23:40, 11. Jun. 2011 (CEST)

