Lösung von Aufgabe 0.2 (SoSe 16)

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

$M_1=\{x|x\in \mathbb{\mathbb{N}}\wedge x+2=0\}$

$M_2=\{x|x\in \mathbb{ℝ}\wedge x^2+2=0\}$

$M_3=\{x|x\in \mathbb{\mathbb{Z}}\wedge x+2=0\}$

$M_4=\{x|x\in \mathbb{\mathbb{Q}}\wedge x^2-2=0\}$

$M_5=\{x|x\in \mathbb{ℝ}\wedge x^2-2=0\}$

$M_6=\{x|x\in \mathbb{ℝ}\wedge (x+2{)}^2=0\}$

$M_1=M_6=\{-2\}$

$M_2=M_3=M_4=\{\}$

$M_5=\{+\sqrt{2};-\sqrt{2}\}$

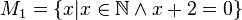
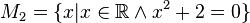
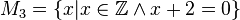
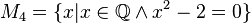
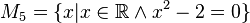
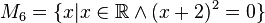
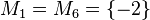
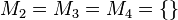
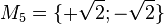
Ich hätte gesagt:

$M_3=M_6=\{-2\}$

$M_1=M_2=M_4=\{\}$

$M_5=\{+\sqrt{2};-\sqrt{2}\}$

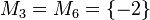
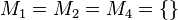
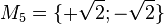
prima!--Schnirch (Diskussion) 13:31, 25. Apr. 2016 (CEST)