Lösung von Aufgabe 1.06 SoSe 2013
AufgabeIn der Differentialgeometrie ist der Begriff der Krümmung einer Kurve von zentraler Bedeutung. Kreise sind Kurven mit konstanter Krümmung, d.h. ein Kreis hat in jedem seiner Punkte dieselbe Krümmung. Je größer ein Kreis
Lösung User ...Es sei K die Krümmung eines Kreises und r sein Radius. Je größer der Radius r wird, desto näher liegt K bei 0. K=1/r --Bushaltefolie 11:29, 14. Mai 2013 (CEST) Lösung User ...Lösung User ... |
 ist, desto mehr nähern sich hinreichend kleine Teilstücke des Kreises Geradenstücken an. Je größer ein Kreis ist, desto geringer ist somit seine Krümmung. Geraden sind auch Kurven konstanter Krümmung, Jede Gerade hat in jedem ihrer Punkte die Krümmung
ist, desto mehr nähern sich hinreichend kleine Teilstücke des Kreises Geradenstücken an. Je größer ein Kreis ist, desto geringer ist somit seine Krümmung. Geraden sind auch Kurven konstanter Krümmung, Jede Gerade hat in jedem ihrer Punkte die Krümmung 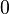 . Geraden könnte man als Kreise mit unendlich großem Radius auffassen. Entwerfen Sie eine sinnvolle Definition des Begriffes Krümmung eines Kreises.
. Geraden könnte man als Kreise mit unendlich großem Radius auffassen. Entwerfen Sie eine sinnvolle Definition des Begriffes Krümmung eines Kreises.
