Lösung von Aufgabe 1.2 (SoSe 21)

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

$M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}$

$M_2 = \{x\vert x\in \mathbb{R}\wedge x^{2}+2 = 0\}$

$M_3 = \{x\vert x\in \mathbb{Z}\wedge x+2 = 0\}$

$M_4 = \{x\vert x\in \mathbb{Q}\wedge x^{2}-2 = 0\}$

$M_5 = \{x\vert x\in \mathbb{R}\wedge x^{2}-2 = 0\}$

$M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}$

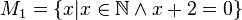
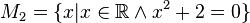
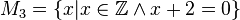
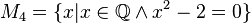
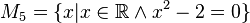
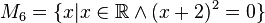
M1={ }

M2={ }

M3={-2}

M4={ }

M5={Wurzel 2, - Wurzel 2}

M6={-2}

--Hippoo (Diskussion) 17:47, 19. Apr. 2021 (CEST)