Lösung von Aufgabe 10.3P (SoSe 12)
Beweisen Sie mit abbildungsgeometrischen Mitteln die Umkehrung des Basiswinkelsatzes.
Darf man die Kongruenzsätze WSW, SSS und so weiter benutzen?--Zitrone 12:34, 24. Jun. 2012 (CEST)
Nein, diese werden wir erst später beweisen und dafür dann vielleicht auf auf diese Sätze zurückgreifen.--Tutorin Anne 19:36, 28. Jun. 2012 (CEST)
ich fang mal mit einem bild an, bei dem die punkte a, b, c beweglich sind:
--Studentin 02:42, 29. Jun. 2012 (CEST)
basiswinkelsatz:
in jedem gleichschenkligen dreieck sind die basiswinkel kongruent zueinander.
umkehrung:
wenn in einem dreieck zwei winkel kongruent zueinander sind, dann handelt es sich um ein gleichschenkliges dreieck
Inhaltsverzeichnis |
Beweis von Studentin
voraussetzung:dreieck hat zwei zueinander kongruente winkeln
behauptung: dreieck ist gleichschenklig
gegeben sei
ein dreieck a, b, c mit zwei kongruenten winkeln alpha und beta,
die mittelsenkrechte m zu (von?) ab und
der schnittpunkt s mit s element von ab und s element von m.
ziel ist es zu zeigen, dass c element von m ist, da denn laut mittelsenkrechtenkriterium |ac| = |bc|
indirekter Beweis der Umkehrung
bei einem indirekten beweis beginne ich mit der annahme, dass |ac| ungleich |bc| sei, c also laut mittelsenkrechtenkriterium nicht auf m läge.
den schnittpunktes von m mit der strecke ac (bzw. der strecke bc - abhängig davon auf welcher halbebenen bezüglich der mittelsenkrechten m der punkt c liegt) nenne ich d.
der abstand des schnittpunktes d zu a und zu b ist gleich groß (wieder mittelsenkrechtenkriterium).
da stellen sich mir zwei fragen:
1.wir wissen wahrscheinlich aber auch noch nichts über die längen der seiten in einem dreieck bzg. ihrer gegenüberliegenden winkel, richtig?
- doch,doch
2. darf ich den basiswinkelsatz nutzen, um die umkehrung zu beweisen?
- Richtig, du darfst den Besisweinkelsatz benutzen, um die Umkehrung zu beweisen. Sehr guter Beweis bis hierher!--Tutorin Anne 22:16, 3. Jul. 2012 (CEST)
bis zur beantwortung versuch ich es mal ohne annahme in einem
direkten beweis
ich weiß, dass folgende spiegelungen gelten:
sm(a)=b und sm(b)=a, da |as|=|bs| und m senkrecht zu ab (def mittelsenkrechte und def geradenspiegelung).
desweiteren sind die winkel alpha und beta kongruent (voraussetzung)
- die Winkel sind kongruent, d.h. ihr Maß ist gleich. Wir wissen aber nicht, ob auch Winkel auch aufeinander abgebildet werden. Ich denke, hier ist das Problem. Da wir dies nicht wissen, können wir auch nicht davon ausgehen, dass sich die Halbgeraden AC+ und BC+ wirklich auf m treffen. Wir können nicht sagen, dass Sm(C)=C ist.--Tutorin Anne 22:16, 3. Jul. 2012 (CEST)
ich weiss nicht richtig, wie ich die halbgeraden ac+ und bc+ auf andere art benennen kann, ohne dass das "c" im namen auftaucht, da ich den punkt c noch nicht brauche. also zum beispiel die halbgerade, die in a beginnt und im winkel alpha zu ab steht (das wäre dann die halbgerade ac+)
kann ich jetzt nicht mit der winkeltreue argumentieren, dass die spiegelung der halbgeraden ac+ an m kongruent zu bc+ sein muss und umgekehrt?
denn wenn ich das könnte, wären der schnittpunkt der beiden halbgeraden auf der mittelhalbierenden (def geradenspiegelung), und dieser schnittpunkt ist punkt c.
da abstände in der geradenspiegelung erhalten bleiben, ist |ac|=|bc|--Studentin 08:34, 29. Jun. 2012 (CEST)
- Herr Schnirch, könnten Sie bitte über diesen Beweis sehen und Stellung dazu nehmen, was ich oben geschrieben habe. Ich bin mir nämlich nicht sicher.--Tutorin Anne 22:16, 3. Jul. 2012 (CEST)
OK, dann schauen wir mal, was wir haben: Ich weiß sicher, dass es eine Spiegelung gibt, die A auf B abbildet und aufgrund der Def. Geradenspiegelung weiß ich auch, dass die Spiegelachse Mittelsenkrechte m zu  ist. Sei M der Mittelpunkt von
ist. Sei M der Mittelpunkt von  . Wegen der Streckentreue und der Def. Geradenspiegelung weiß ich dann auch, dass
. Wegen der Streckentreue und der Def. Geradenspiegelung weiß ich dann auch, dass 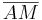 auf
auf 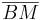 abgebildet wird. Wegen der Winkeltreue und der Tatsache, dass
abgebildet wird. Wegen der Winkeltreue und der Tatsache, dass  Teilmenge der Schenkel
Teilmenge der Schenkel  und
und 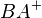 der beiden Winkel
der beiden Winkel  und
und  sind, muss
sind, muss  bei der Spiegelung an m auf den kongruenten Winkel
bei der Spiegelung an m auf den kongruenten Winkel  abgebildet werden. Wir wissen außerdem, dass sich die beiden anderen Schenkel von
abgebildet werden. Wir wissen außerdem, dass sich die beiden anderen Schenkel von  und
und  im Punkt C schneiden, da wir ja ein Dreieck
im Punkt C schneiden, da wir ja ein Dreieck  voraussetzen. Die entscheidende Frage ist nun: Wie können wir jetzt begründen, dass C auf m liegen muss? Wenn Sie das schaffen, ist der Beweis fertig!--Schnirch 13:46, 4. Jul. 2012 (CEST)
voraussetzen. Die entscheidende Frage ist nun: Wie können wir jetzt begründen, dass C auf m liegen muss? Wenn Sie das schaffen, ist der Beweis fertig!--Schnirch 13:46, 4. Jul. 2012 (CEST)
müssen wir das noch beweisen?
wir wissen doch, dass sich die halbgeraden spiegeln, und dass sie sich in irgendeinem punkt mit m schneiden. dieser punkt ist element von m, und daher ist es fixpunkt bezüglich der geradenspiegelung (nennen wir ihn c).
wo ist mein denkfehler???--Studentin 16:06, 4. Jul. 2012 (CEST)
- richtig, wir wissen, die sich die halbgeraden AC+ und BC+ schneiden. Aber das C auf m liegt, dass muss erst noch begründet werden. Die Begründung hast du gerade schon genannt, aber die Reihenfolge der aufeinander folgenden Schritte ist so nicht richtig.--Tutorin Anne 09:14, 7. Jul. 2012 (CEST)
ich hab es so gemeint:
der punkt, an dem sich die eine halbgerade mit m schneidet, ist fixpunkt bezüglich der geradenspiegelung
die gepiegelte halbgerade hat also auch den schnittpunkt mit m an diesem gleichen punkt.
in diesem punkt schneiden sich also auch die beiden halbgeraden.
da der schnittpunkt der beiden halbgeraden gleich dem schnittpunkt der halbgeraden mit m ist, liegt der schnittpunkt auf m.--Studentin 11:57, 8. Jul. 2012 (CEST)
OK, das ist jetzt in Ordnung!--Schnirch 15:15, 9. Jul. 2012 (CEST)
Beweis von Fahrtwind und Honeydukes
Voraussetzung: in einem Dreieck sind zwei Winkel kongruent zueinander; <MAC ist kongruent zu <MBC und m ist Spiegelgerade Sm
Behauptung: Dreieck ist gleichschenklig -> |AC| = |BC|
| Beweisschritt | Begründung |
|---|---|
(1) 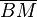 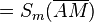 |
Vor., Geradenspiegelung |
(2)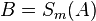 |
Geradenspiegelung |
(3)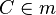 mit m ist Mittelsenkrechte von mit m ist Mittelsenkrechte von  |
Vor., Mittelsenkrechtenkriterium |
(4) 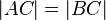 |
Mittelsenkrechtenkriterium |
Ist das so in Ordnung? Und, darf ich bei (3) einfach annehmen, dass C Element von m ist? --Fahrtwind 18:18, 30. Jun. 2012 (CEST)
Ich denke schon. Ich habe es so ähnlich. Schritt eins und zwei ist identisch. Dann...
Schritt drei ist: "m= Mittelsenkrechte von Strecke AB" (Begr.: Def. Mittelsenkr. und Vorauss.).
- Das m die Mittelsenkrechte ist, habt ihr ja schon für Schritt 1) und 2) verwendet, ohne die Verwendung zu nennen.--Tutorin Anne 22:29, 3. Jul. 2012 (CEST)
Schritt vier ist: "Es existiert ein C Element m" (Begr.: Def. Mittelsenkr.)
Schritt fünf ist: "Abstand AC = Abstand BC" (Begr.: Schritt 4, Mittelsenkrechtenkrit., abstandserhaltend [Sm (AC)= BC] --Honeydukes 17:56, 2. Jul. 2012 (CEST)
- Ihr könnt nicht davon ausgehen, dass C als Eckpunkt des Dreiecks auf der Mittelsenkrechten liegt. Deshalb ist der Beweis so nicht richtig. --Tutorin Anne 22:29, 3. Jul. 2012 (CEST)
Beweisschritte, Begründung bitte zufügen
Hier gebe ich mal eine Möglichkeit eines direkten Beweises vor. Ergänzt die Beweisschritte.--Tutorin Anne 22:29, 3. Jul. 2012 (CEST)
| Voraussetzung | Dreieck  mit üblicher Bezeichnung, mit üblicher Bezeichnung, 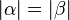
|
| Behauptung | 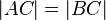
|
Vorschlag Fahrtwind
| Beweisschritt | Begründung |
|---|---|
1) m ist Mittelsenkrechte von  |
(Vor, Def. Mittelsenkrechte) |
2) 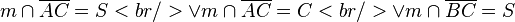 |
(Satz vom Pasch oder C auf m (weil noch eine weitere Seite geschnitten wird - aber passt das, weil m in einem Fall durch den Eckpunkt C verläuft?- Ja, das ist in Ordnung - aber du hast gut aufgepasst!) |
3) FAll 1)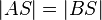 |
(Mittelsenkrechtenkriterium) |
4) 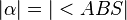 |
(Vor., 3.) Warum aus 3. - Begründung? |
5) 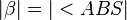 |
(Vor., 3.) Warum das? |
6) 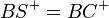 |
(Def. Winkel, 4.,5.) |
7) 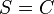 |
(4.,5.,6.) Wozu braucht man hier die Winkelgrößen? |
8) 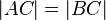 |
(Mittelsenkrechtenkriterium), aus welchem Schritt wurde das abgeleitet?? |
| 9) Fall 2) analog Fall 1 | - |
10) Fall 3) 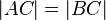 |
(Mittelsenkrechtenkriterium) |
- Die Begründungen stimmen so nicht alle. Schaut nochmal bei 4), 5),7), 8) - teilweise ist es einfach zu viel, teilweise fehlt was, teilweise ist die Begründung falsch.--Tutorin Anne 15:11, 4. Jul. 2012 (CEST)
Ich hab mich nochmal mit der Begründung versucht...
- Die Begründungen sind bei 4,5,7,8 noch nicht richtig. Ich habe mal Fragen hinzugefügt.--Tutorin Anne 09:19, 7. Jul. 2012 (CEST)
| Beweisschritt | Begründung |
|---|---|
1) m ist Mittelsenkrechte von  |
(Vor, Def. Mittelsenkrechte) |
2) 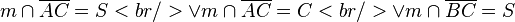 |
(Satz vom Pasch oder C auf m (weil noch eine weitere Seite geschnitten wird - aber passt das, weil m in einem Fall durch den Eckpunkt C verläuft?- Ja, das ist in Ordnung - aber du hast gut aufgepasst!) |
3) FAll 1)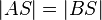 |
(Mittelsenkrechtenkriterium) |
4) 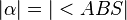 |
(3.) Basiswinkelsatz |
5) 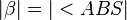 |
(Vor., 4.) |
6) 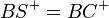 |
(Def. Winkel, 5.) |
7) 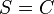 |
(2.,6.) Da S und C jeweils Schnittpunkte der Graden AC und BC mit m sind. |
8) 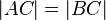 |
(3.,7.) |
| 9) Fall 2) analog Fall 1 | - |
10) Fall 3) 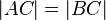 |
(Mittelsenkrechtenkriterium) |
q.e.d.--Tutorin Anne 08:50, 10. Jul. 2012 (CEST)
Ich habe noch eine wichtige Frage:
Was genau bedeutet es, wenn wir mit "abbildungsgeometrischen Mitteln" etwas beweisen sollen? Heißt es, dass wir nur mit Spiegelungen beweisen sollen? Oder was können wir alles benutzen bzw. was nicht?
--Fahrtwind 20:12, 21. Jul. 2012 (CEST)
Danke für die wirklich gute Frage.
Also, abbildungsgeometrische Mittel heißt schon, dass man über Spiegelungen/ Drehungen etc. gehen soll und dann die Eigenschaften dieser Abbildungen nutzen muss. Dies ist z.B. beim Beweis von Studentin der Fall.
Die unteren Beweise, die so richtig sind, sind streng genommen aber nicht speziell abbildungsgeometrisch, da sie nur auf Sätze aufbauen, nicht aber auf Abbildungen und deren Eigenschaften.Beim Lösen der Aufgabe haben wir Tutoren uns auch nicht an abbildungsgeometische Mittel gehalten.--Tutorin Anne 16:33, 22. Jul. 2012 (CEST)

