Lösung von Aufgabe 11.2P (SoSe 20)

Beweisen Sie Satz IX.9:
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Jeder Punkt P hat dabei zu seinem Bildpunkt $P''=S_{a}\circ S_{b}(P)$ einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.

Voraussetzung: 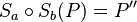$S_a\circ S_b(P)=P''$, mit $a| | b$

Behauptung: 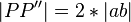$|PP''| =2*|ab|$

	Beweisschritt	Begründung
1)	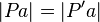$|Pa| = |P'a|$	Eigenschaft Geradenspiegelung
2)	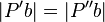$|P'b| = |P''b|$	Eigenschaft Geradenspiegelung
3)	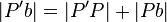$|P'b| = |P'P|+|Pb|$	Skizze (wenn gezeichnet, ist das klar)
4)	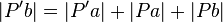$|P'b| = |P'a|+|Pa|+|Pb|$	1), 3), Skizze
5)	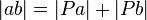$|ab| = |Pa|+|Pb|$	Skizze
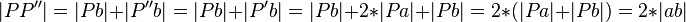6)	$|PP''| = |Pb|+|P''b|= |Pb|+|P'b|=|Pb|+2*|Pa|+|Pb|=2*(|Pa|+|Pb|)=2*|ab|$	Skizze, 2), 4), 5)

--tgksope (Diskussion) 11:24, 25. Jul. 2020 (CEST)

Mit einer Skizze zu Begründen ist schwierig. Es wäre korrekt, wenn du mathematische Begründungen aufführt.
Die Beweise ähneln sich. 

Voraussetzung: $a || b ,   S_a\circ S_b , P''= S_a\circ S_b(P)  ,S_1 \in \overline { PP' },  S_2 \in \overline { P'P'' },  S_1 \in a \wedge S_2 \in b$ 
Behauptung:$|PP''| =2\cdot|ab|$

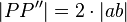
	Beweisschritt	Begründung
1)	$|PS_1|= |P'S_1|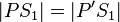$	Def. Geradenspiegelung (GS), Abstandserhaltung der GS
2)	$|P'S_| = |P''S_2|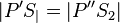$	Def. Geradenspiegelung (GS), Abstandserhaltung der GS
3)	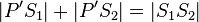$|P'S_1| + |P'S_2|= |S_1 S_2|$	Addition von Abständen
4)	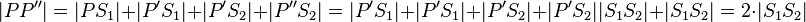$|PP''| = |PS_1| + |P'S_1| + |P'S_2| + |P''S_2| = |P'S_1| + |P'S_1| + |P'S_2| + |P'S_2| |S_1S_2| + |S_1S_2| = 2 \cdot |S_1S_2|$	1), 2), 3), Addition von Abständen, Rechnen in R

Eine Skizze ist immer nur für uns zum Verständnis wichtig. Vielleicht kannst du die passende Skizze zu diesem Beweis zeichnen,
um den Beweis besser nachvollziehen zu können. Falls nicht stelle ich noch ein Bild ein.--Tutorin Laura (Diskussion) 11:31, 27. Jul. 2020 (CEST)