Lösung von Aufgabe 13.2P (WS 18/19)
Aus Geometrie-Wiki
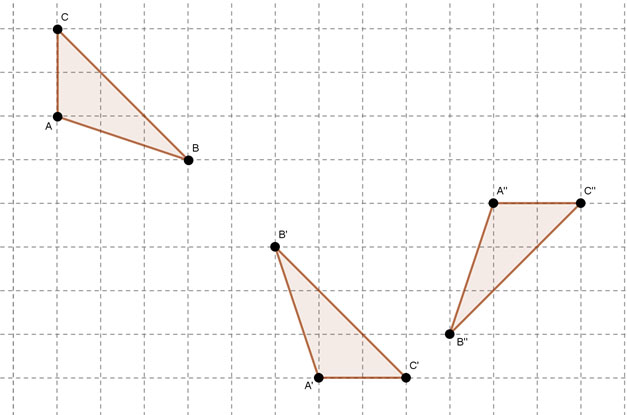
Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen 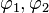 , mit
, mit 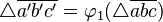 und
und 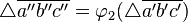 .
.
- wie heißen die beiden Abbildungen
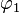 und
und 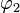 ?
?
- Zeichnen Sie jeweils für
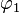 und
und 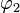 die passende Anzahl von Spiegelachsen in die Skizze ein.
die passende Anzahl von Spiegelachsen in die Skizze ein.
- Durch welche Ersatzabbildung kann die Verkettung
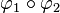 ersetzt werden (Begründen Sie Ihre Entscheidung)?
ersetzt werden (Begründen Sie Ihre Entscheidung)?
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze ein.
1. φ1: Geradenspiegelung (pink); φ2: Schubspiegelung (orange)
2.
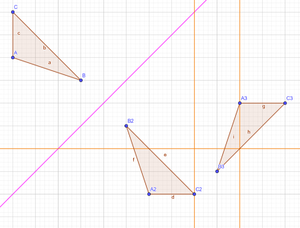
3. Sa Sb
Sb Sc
Sc Sd mit |orientierter Winkel ab| = 45 und b ist senkrecht zu c und c || d
Sd mit |orientierter Winkel ab| = 45 und b ist senkrecht zu c und c || d
= Sa' Sb'
Sb' Sc
Sc Sd mit |orientierter Winkel a'b'| = 45 und b' || c - Eigeschaft Schubspiegelung und Drehung
Sd mit |orientierter Winkel a'b'| = 45 und b' || c - Eigeschaft Schubspiegelung und Drehung
= Sa' Sb'
Sb' Sc'
Sc' Sd' mit |cd| = |c'd'| und c'=b' - Eigenschaft Verschiebung
Sd' mit |cd| = |c'd'| und c'=b' - Eigenschaft Verschiebung
= Sa' Sd' mit |orientierter Winkel a'd'| = 45 - Stufenwinkelsatz, Identität b',c'
Sd' mit |orientierter Winkel a'd'| = 45 - Stufenwinkelsatz, Identität b',c'
= DP,90 mit a' geschnitten d' = P
4.(N sei P aus 3.)
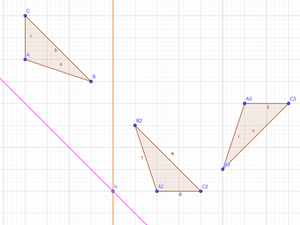
--CIG UA (Diskussion) 12:20, 25. Jan. 2019 (CET)