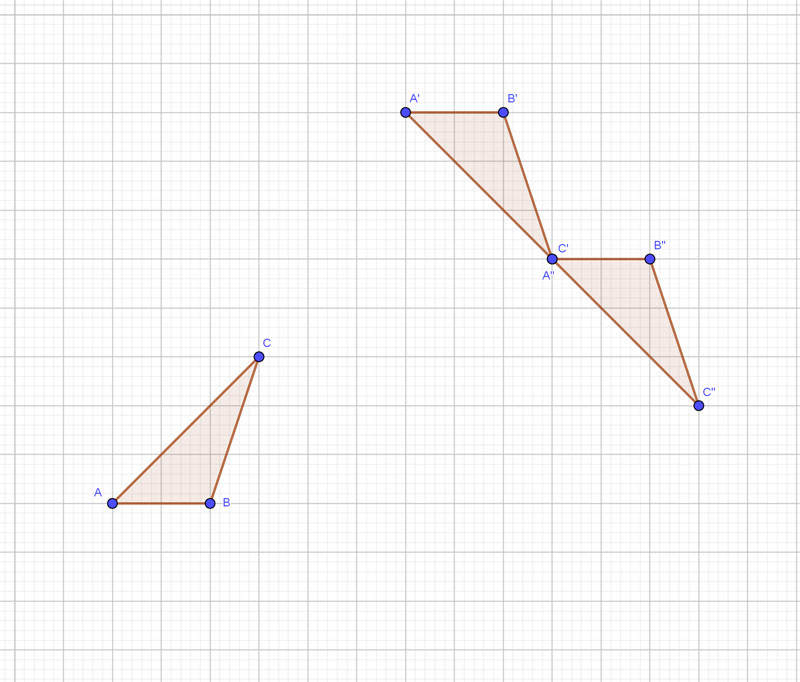
Lösung von Aufgabe 13.3P (WS 17 18)
Aus Geometrie-Wiki
Dargestellt ist hier die Nacheinanderausführung zweier Abbildungen 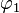 und
und 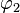 , mit
, mit 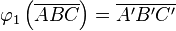 und
und 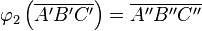 .
.
- Um welche Arten von Abbildungen handelt es sich bei
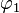 und
und 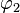 ?
?
- Zeichnen Sie jeweils für
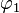 und
und 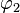 die passende Anzahl von Spiegelachsen in die Skizze ein.
die passende Anzahl von Spiegelachsen in die Skizze ein.
- Wir betrachten nun die Verkettung
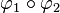 . Durch welche Ersatzabbildung kann diese Verkettung
. Durch welche Ersatzabbildung kann diese Verkettung 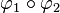 ersetzt werden? (Begründen Sie Ihre Entscheidung).
ersetzt werden? (Begründen Sie Ihre Entscheidung).
- Zeichnen Sie die Achsen der Ersatzabbildung in die Skizze oben ein. Hinweis: Sie dürfen das Gitter im Hintergrund als Orientierung nutzen.