Lösung von Aufgabe 13.6
Inhaltsverzeichnis |
Aufgabenstellung:
Frau Schultze-Kröttendörfer räumt ihren Schrank auf. Es findet sich ein Stapel Arbeitsblätter, auf die ein Parallelogramm gedruckt wurde, welches keine Raute ist. "Zu dumm", denkt Frau Schultze-Kröttendörfer, "ich brauche Arbeitsblätter mit Rauten". Kurz darauf kommt ihr eine zündende Idee. Sie wird den Begriff der Raute konstruktiv erarbeiten lassen. Diesbezüglich wird sie den Schülern den Auftrag geben, die Parallelogramme auf den vorhandenen Arbeitsblättern auszuschneiden und dann so zu falten, dass zwei benachbarte Seiten des Parallelogramms zur Deckung kommen. Erläutern Sie wie und beweisen Sie dass die Schüler von Frau Schultze-Kröttendörfer durch die genannten Faltungen aus den Parallelogrammen Rauten generieren.
Skizze:
Anstatt einer Faltung kann man in diesem Applet die Punkte 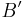 (auf
(auf 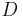 ) und
) und 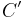 (auf
(auf  ) bewegen. Man stelle sich die Faltung über die (gestrichelte) Winkelhalbierende jeweils analog vor.
) bewegen. Man stelle sich die Faltung über die (gestrichelte) Winkelhalbierende jeweils analog vor.
Beweis:
Voraussetzung:
- Parallelogramm

- Ein Parallelogramm sei ein Viereck mit zwei Paar parallelen Seiten
- Die parallelen Seiten sind gleich groß (Das kann bewiesen werden: Beweis Teil 2)
Behauptung:
- Konstruktion einer Raute aus Parallelogramm
- Eine Raute sei ein Viereck bei dem alle vier Seiten gleich groß sind.
- Die gegenüberliegenden Seiten (die Seiten, die keinen Eckpunkt gemeinsam haben) sind parallel zueinander (Auch das kann beweisen werden: Beweis Teil 3)
Formloser Beweis:
Wenn Frau Schultze-Kröttendörfer eine Seite, die kürzer ist als ihre Nachbarseite (eine Seite mit gemeinsamen Endpunkt) auf die (längere) Nachbarseite faltet (die Winkelhalbierende des Winkels am gemeinsamen Punkt sei die Faltlinie), so erhält man (wenn diese Faltung mit der selben kurzen Seite zweimal stattfindet) zwei Punkte auf den langen Seiten. Diese Punkte verbindet man und erhält eine "neue" kurze Seite, die wiederum parallel zur ersten kurzen Seite ist. Durch die Faltung haben wir auf der langen Seite einen Punkt, der vom (mit der gefalteten Seite gemeinsamen) Eckpunkt so weit entfernt ist, wie der zweite Eckpunkt der gefalteten Seite. Klingt kompliziert, einfach gesprochen: die langen Seiten sind so lang wie die kurze Seite (durch Faltung). Die beiden kurzen Seiten sind weiterhin parallel zueinander (siehe Beweis Teil 3) und ohnehin gleich lang. Wir haben vier gleichlange Seiten erhalten!
-- Kleine Anmerkung: was ist, wenn es keine längeren / kürzeren Seiten gibt, wenn also selbst nicht zueinander parallele Seiten gleich lang sind? .... --
Beweis Teil 2:
Die parallelen Seiten in einem Parallelogramm sind gleich groß.
Äquivalente Behauptung: der Abstand aller Punkte der Geraden  zu einer zu
zu einer zu  parallelen Geraden
parallelen Geraden  ist gleich groß.
ist gleich groß.
- Ist die zweite Behauptung tatsächlig äquivalent zur ersten Behauptung?
- Der Beweis an sich!
Beweis Teil 3:
Die gegenüberliegenden Seiten einer Raute sind parallel zueinander.
Äquivalente Behauptung: Wenn die Punkte  und
und  zueinander den selben Abstand haben wie
zueinander den selben Abstand haben wie  und
und 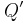 , so sind die Geraden
, so sind die Geraden 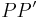 und
und 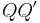 parallel, wenn die Halbebenen
parallel, wenn die Halbebenen 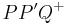 und
und 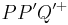 identisch sind.
identisch sind.
- Ist die zweite Behauptung tatsächlig äquivalent zur ersten Behauptung?
- Der Beweis an sich!
- Warum der ganze Mist?
- tbc
- to be continued
- Hier sei auf den Unterschied von Definitionen (Festlegungen, die sinnvoll und sinnlos sein können) und Sätzen verwiesen. Bei den Übungsklausuren kamen immer wieder Transfer-Aufgaben, die sich um ein Parallelogramm oder ein Trapez oder eine Raute drehten. Da ist es oftmals einfacher, wenn man sich vor Augen führt, was definiert ist und was wir beweisen können (letzteres läuft auf "SÄTZE" hinaus und wird in Wikipedia zu den Definitionen gezählt...).

