Aufgabe 2.10 SoSe 2018
Es seien  eine Gerade und eine Gerade und  ein Punkt außerhalb von ein Punkt außerhalb von  . Ferner sei . Ferner sei  eine Gerade die senkrecht auf eine Gerade die senkrecht auf  steht und durch steht und durch  geht. Beweisen Sie: Es gibt keine weitere von geht. Beweisen Sie: Es gibt keine weitere von  verschiedene Gerade, dir ebenfalls senkrecht auf verschiedene Gerade, dir ebenfalls senkrecht auf  steht und durch steht und durch  geht. geht.
Hinweis: Es handelt sich um einen "Highlanderbeweis" (Es kann nur einen geben: Highlander - Es kann nur einen geben). In der Regel führt man derartige Eindeutigkeitsbeweise als Widerspruchsbeweise.
Lösung
Es seien  eine Gerade und eine Gerade und 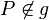 ein Punkt. Wir nehmen an, dass zwei verschiedene Geraden ein Punkt. Wir nehmen an, dass zwei verschiedene Geraden 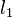 und und 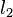 existieren, die durch existieren, die durch  gehen und senkrecht auf gehen und senkrecht auf  stehen. stehen. 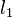 habe mit habe mit  den Punkt den Punkt 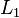 gemeinsam, der Schnittpunkt von gemeinsam, der Schnittpunkt von 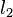 mit mit  sei mit sei mit 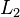 bezeichnet. Weil sowohl bezeichnet. Weil sowohl 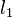 als auch als auch 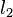 senkrecht auf senkrecht auf  steht, hat das Dreieck steht, hat das Dreieck 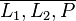 zwei rechte Winkel. Das ist ein Widerspruch zum Innenwinkelsatz für Dreiecke. zwei rechte Winkel. Das ist ein Widerspruch zum Innenwinkelsatz für Dreiecke.
|