Lösung von Aufgabe 3.3
Wir gehen von folgender Definition aus:
Eine Winkelhalbierende eines Winkels  ist ein Strahl l, der im Inneren des Winkels
ist ein Strahl l, der im Inneren des Winkels  liegt, den Scheitel des Winkels
liegt, den Scheitel des Winkels  als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel
als Anfangspunkt besitzt und diesen Winkel in zwei gleich große Winkel 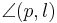 und
und 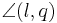 unterteilt.
unterteilt.
Außerdem sei folgende genetische Definition gegeben:
- Gegeben sei ein Winkel
 .
.
- Man konstruiere auf den beiden Schenkeln des Winkels
 zwei Punkte P und Q, die vom Scheitel S des Winkels
zwei Punkte P und Q, die vom Scheitel S des Winkels  gleich weit entfernt sind.
gleich weit entfernt sind.
- Man konstruiere die Strecke
 .
.
- Man konstruiere den Mittelpunkt M der Strecke
 .
.
- Man konstruiere den Strahl w mit dem Anfangspunkt S, der durch den Punkt M verläuft.
- Dieser Strahl w ist die Winkelhalbierende.
Beweisen Sie, dass durch diese Konstruktionsvorschrift tatsächlich die Winkelhalbierende entsprechend der angegebenen Definition entsteht.
Die Lösung von Engel82 ist korrekt!
zur Anmerkung von Vollyschwamm: Wir gehen von der Definition Winkelhalbierende aus.
Jede weitere "Definition" des Begriffs Winkelhalbierende (auch eine Konstruktionsvorschrift) lässt sich dann als Satz beweisen,
da man immer eine Äquivalenz zur ersten Definition zeigen kann!--Schnirch 13:33, 22. Nov. 2010 (UTC)
VSS: Winkel pq, Anfangspunkt S, Strecke SP=Strecke SQ, Strecke PM=Strecke MQ.
Beh: Winkel PSM=Winkel MSQ
1. SP=SQ; VSS; (Konstruktion)
2. PM=MQ; VSS;(Konstruktion), da M Mittelpunkt von der Strecke PQ ist
3. SM=SM; trivial
4. Dreick SPM= Dreieck SMQ; SSS und 1.,2., 3.
5. Winkel PSM= Winkel MSQ; 4.
6. Strahl SM* ist Winkelhalbierende
--Engel82 09:02, 28. Okt. 2010 (UTC)
Wie beweisen? Ich dachte das soll eine Definition bzw. Konstruktionsanleitung sein und solche kann man nicht beweisen, die sind nur sinnvoll oder eben nicht?!--Vollyschwamm 18:19, 1. Nov. 2010 (UT
Ich denke, man muss zeigen, dass das die Winkelhalbierende, die laut Konstrunktionsanleitung entstanden ist, den Winkel in pq in zwei gleichgroße Winkel teilt. Wenn man sich für eine Definition entschieden hat, kann man die andere ja immer beweisen (wobei die andere Definition dann ein Satz ist).Verteidigungswolf

