Lösung von Aufgabe 4.3 P (SoSe 14)
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
a) Wenn eine Gerade senkrecht auf einer Strecke steht, und diese halbiert, dann ist die Gerade die Mittelsenkrechte der Strecke.
b) Wenn alle Punkte einer Menge von den Endpunkten einer Strecke ein und denselben Abstand haben, dann ist diese Menge die Mittelsenkrechte der Strecke. --Audrey Hepburn (Diskussion) 12:21, 20. Mai 2014 (CEST)
Bei deiner b) Version sehe ich noch das Problem, dass deine benannte Menge auch eine "löchrige" Gerade oder eine Strecke sein könnte. --Tutorin Anne (Diskussion) 19:09, 20. Mai 2014 (CEST)
Wenn eine Gerade m eine Strecke s mit den Punkten A und B senkrecht im Punkt P so teilt, dass gilt: 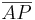 =
= 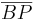 , dann heißt m Mittelsenkrechte der Strecke s. --The Niggster (Diskussion) 18:06, 21. Mai 2014 (CEST)
, dann heißt m Mittelsenkrechte der Strecke s. --The Niggster (Diskussion) 18:06, 21. Mai 2014 (CEST)
Die Definition entspricht der a) Version von Audrey Hepburn. Sie ist sehr genau beschrieben, das ist super. Allerdings würde ich die Strecke  nennen, damit auch klar ist, dass es sich bei A und B um die Endpunkte der Strecke handelt. --Tutorin Anne (Diskussion) 23:08, 22. Mai 2014 (CEST)
nennen, damit auch klar ist, dass es sich bei A und B um die Endpunkte der Strecke handelt. --Tutorin Anne (Diskussion) 23:08, 22. Mai 2014 (CEST)

