Lösung von Aufgabe 4.3 P (WS 13/14)
Aus Geometrie-Wiki
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Hier zwei Vorschläge:
1. Gegeben sei eine Strecke  und eine Gerade m, die die Strecke
und eine Gerade m, die die Strecke  im Punkt M schneidet. Wenn m
im Punkt M schneidet. Wenn m  in zwei gleichlange Strecken
in zwei gleichlange Strecken 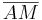 und
und  teilt und auf
teilt und auf  senkrecht steht, dann nennt man m die Mittelsenkrechte von
senkrecht steht, dann nennt man m die Mittelsenkrechte von  .
.
- Die Definition ist schon sehr gut. Allerdings kann ein Gerade oder sonst etwas nicht einfach senkrecht stehen. Senkrecht ist ein Begriff einer Relation d.h. es bezieht sich immer auf zwei Dinge: A steht senkrecht zu/ auf b.--Tutorin Anne (Diskussion) 18:29, 7. Jan. 2014 (CET)
2. Gegeben sei eine Strecke  und eine Gerade m, die die Strecke
und eine Gerade m, die die Strecke  schneidet. Wenn eine Geradenspiegelung an m den Punkt A auf A' derart abbildet, dass A'=B ist, dann nennt man m die Mittelsenkrechte von
schneidet. Wenn eine Geradenspiegelung an m den Punkt A auf A' derart abbildet, dass A'=B ist, dann nennt man m die Mittelsenkrechte von  .--EarlHickey (Diskussion) 22:15, 6. Jan. 2014 (CET)
.--EarlHickey (Diskussion) 22:15, 6. Jan. 2014 (CET)
- Sehr gute Idee und auch richtig. Allerdings informell... du nennst mehr Informationen als nötig. Welche kannst du weglassen?--Tutorin Anne (Diskussion) 18:29, 7. Jan. 2014 (CET)

