Aufgabe 5.10
Es seien 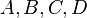 vier paarweise verschiedene Punkte. vier paarweise verschiedene Punkte.
Beweisen Sie:
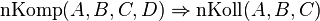
Lösung von Aufgabe 5.10 S SoSe 13
Lösung User --Illu13 00:24, 31. Mai 2013 (CEST)
Je drei der vier Punkte dürfen nicht kollinear sein, da sie sonst mit dem vierten Punkt immer in ein und derselben Ebene liegen würden und somit komplanar wären. Dies ist aber ein Widerspruch zur Voraussetzung nkomp(A,B,C,D).
Nach Axiom I/4 bilden die Punkte A,B,C eine Ebene E, welche Punkt D nicht enthält. Wenn Punkt D auch in dieser Ebene liegen würde, dann wären die vier Punkte wieder komplanar, was unserer Voraussetzung widersprechen würde.
nkomp(A,B,C,D)  (nach Definition I/4 und Axiom I/4) (nach Definition I/4 und Axiom I/4)  Ebene E: A,B,C Ebene E: A,B,C  E E 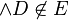
Annahme: koll(A,B,C)   Gerade g: A,B,C Gerade g: A,B,C  g g
D 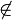 g g   Ebene F: D Ebene F: D  F F  g g  F F  A,B,C,D A,B,C,D  F F  komp(A,B,C,D) komp(A,B,C,D)  Widerspruch zur Voraussetzung Widerspruch zur Voraussetzung
 nkoll(A,B,C) q.e.d. nkoll(A,B,C) q.e.d.
--Illu13 00:24, 31. Mai 2013 (CEST)
Bemerkung --*m.g.* 23:45, 3. Jun. 2013 (CEST)
- Sie haben die Beweisidee erkannt und das Prinzip des Beweises gut in den ersten Worten illustriert.
- nkomp(A,B,C,D)
 (nach Definition I/4 und Axiom I/4) (nach Definition I/4 und Axiom I/4)  Ebene E: A,B,C Ebene E: A,B,C  E E 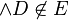 , ,
nach Definition I/4 hat hier nichts verloren, Sie können aus einer Definition nicht die Existenz von etwas schließen. Schreiben Sie doch einfacher, dass Sie davon ausgehen, dass D nicht in der Ebene ABC liegt. (eigentlich wäre hier eine Fallunterscheidung angesagt. s. Übung
- Das sollten Sie noch einmal formulieren:
D 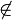 g g   Ebene F: D Ebene F: D  F F  g g  F F  A,B,C,D A,B,C,D  F F  komp(A,B,C,D) komp(A,B,C,D)  Widerspruch zur Voraussetzung Widerspruch zur Voraussetzung
Lösung User ...
Lösung User ...
zurück zu Serie 5 SoSe 2013
|
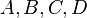 vier paarweise verschiedene Punkte.
vier paarweise verschiedene Punkte.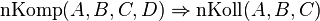
 (nach Definition I/4 und Axiom I/4)
(nach Definition I/4 und Axiom I/4)  Ebene E: A,B,C
Ebene E: A,B,C  E
E 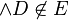
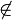 g
g  g
g 
