Lösung von Aufgabe 8.1P (SoSe 22)
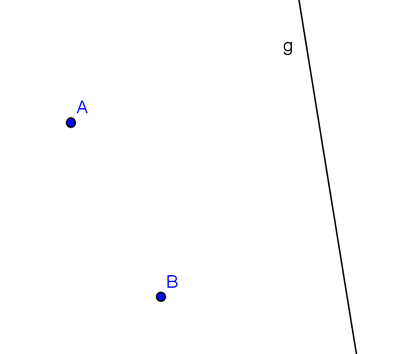
Das klassische Feuerwehrproblem: Am Punkt A steht die Feuerwehr, Punkt B symbolisiert das brennende Haus. Die Gerade g ist die Uferbegrenzung eines Flusses, aus dem die Feuerwehr das Wasser holen muss. Welchen Weg muss die Feuerwehr nehmen um Löschwasser am Fluss zu tanken um danach möglichst schnell am brennenden Haus zu sein? Konstruieren Sie nachstehend die optimale Route für die Feuerwehr und begründen Sie Ihre Konstruktion.
Das Problem lässt sich auf viele verschiedene Anwendungen übertragen, z. B.:
- reitende Cowboys, die ihr Pferd noch tränken müssen, bevor sie den Salon in Doce City erreichen
- Lichtstrahlen, die am Spiegel g reflektiert werden und immer den kürzesten Weg nehmen
- Billardkugeln, die durch einen zentralen Stoß und über Bande g einander treffen sollen
- ...
der kürzeste Weg für die Feuerwehr zum Bach und dann zum brennenden Haus ist der Weg über einen Punkt C auf der Geraden g und dann von Punkt C zu Punkt B. Punkt C auf g erhalte ich durch die Spiegelung des Punktes A auf A` an der Geraden g und wenn ich dann A` dann mit dem Punkt B verbinde, und dessen Schnittpunkt als C benenne.
Begründung: die kürzeste Verbindung zwischen B und A` ist die Strecke BA`
aufgrund der Längentreue der Geradenspiegelung Sg, welche besagt, dass die Länge der Strecke A`C genauso lang ist wie die Länge der Strecke AC, da der Punkt A` bei der Spiegelung an g den gleichen Abstand zu g hat wie Punkt A zu g
daraus folgt : Strecke AC + Strecke BC = Strecke BA`--Kwd077 (Diskussion) 15:48, 13. Jun. 2022 (CEST)
richtig--Matze2000 (Diskussion) 16:45, 16. Jun. 2022 (CEST)