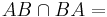Lösung von Aufgabe 8.2 (WS 12 13)
Aus Geometrie-Wiki
Aufgabe 8.1Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen? a) b) c) d)
User Caro44Lösung 8.2Student XY bezieht sich bei seiner Argumentation nur auf zwei festgelegte Punkte, nämlich A und B. Damit die Figur jedoch konvex ist bzw. seine Argumentation stimmt, muss die Voraussetzung für alle Punkte der Figur gelten.
Lösung Sissy66Definition "konvexe Punktmenge" sagt aus, dass eine Menge M von Punkten dann konvex heißt, wenn mit JE zwei Punkten A und B dieser Menge die gesamte Strecke AB zu M gehört. In seinen Überlegungen hat er nicht alle Punkte mit einbezogen. --Sissy66 09:52, 19. Dez. 2012 (CET) |
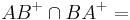
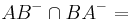
 geschnitten mit dem Kreis um
geschnitten mit dem Kreis um  durch
durch  =
=