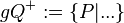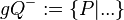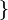Aufgabe 8.4
Ergänzen Sie die Definition für offene Halbebenen  und und 
("Offen" bedeutet hier: Die Halbebene ohne die Gerade, die die Ebene teilt).
Definition (offene Halbebene):
- Es sei E eine Ebene, in der die Gerade g und der Punkt Q liegen mögen. Q gehöre nicht zu g. Unter den offenen Teilmengen
 und und  bezüglich der Trägergeraden g versteht man die folgenden Teilmengen von E: bezüglich der Trägergeraden g versteht man die folgenden Teilmengen von E:
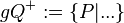
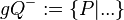
Lösung von User Caro44
Fehler beim Parsen(Syntaxfehler): \ gQ+:= \{P|\overline{PQ} \cap g = \{ }
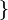
Fehler beim Parsen(Syntaxfehler): \ gQ-:= \{P|\overline{PQ} \cap g = \{S}
--Caro44 21:06, 15. Dez. 2012 (CET)
Die Gerade g muss bei der Halebene gQ- noch abgezogen werden, ansonsten wäre es eine geschlossene Halbebene.
--Yellow 12:25, 18. Dez. 2012 (CET)
Lösung von Sissy66
Müsste man nicht noch dazu sagen, dass der Punkt P Element der Ebene ohne die Gerade g ist?
--Sissy66 10:38, 19. Dez. 2012 (CET)
|  und
und