Lösung von Zusatzaufgabe 1 (SoSe 13)
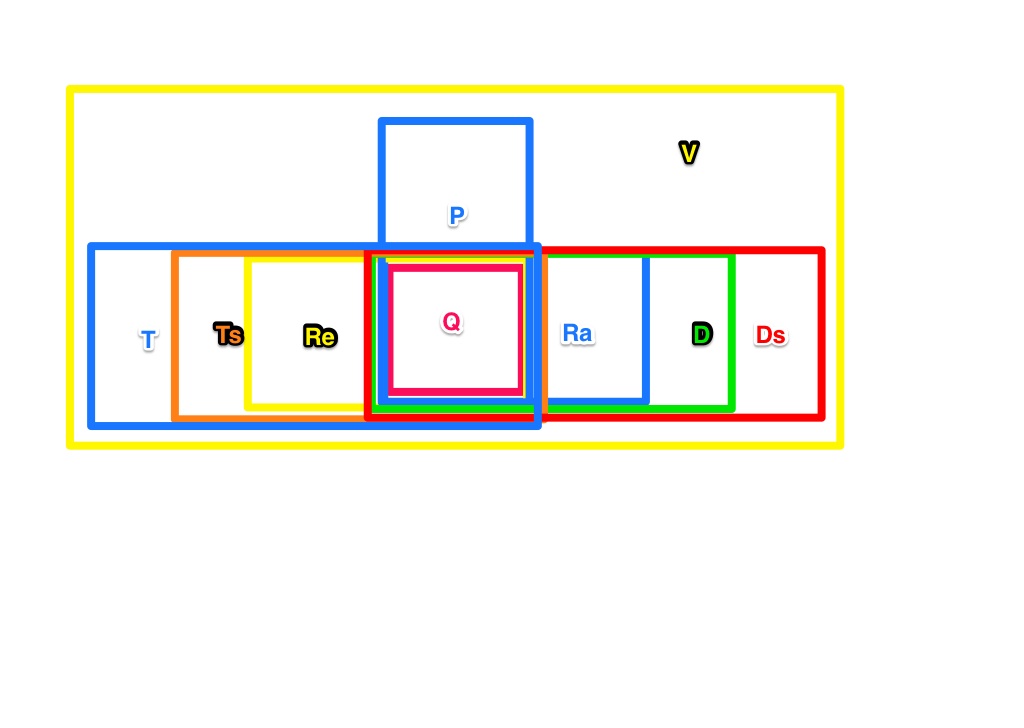
Erstellen Sie zu den Vierecksarten aus Aufgabe 1.2 ein Venndiagramm, aus dem die Teilmengenbeziehungen der Mengen sichtbar werden.
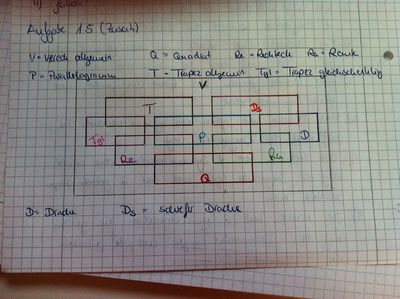
Ist das ein Venn-Diagramm?--Audrey Hepburn 20:54, 24. Apr. 2013 (CEST)
erstmal vielen Dank für diese Lösung. Das ist ein super Venn-Diagramm. Inhaltlich lässt sich das Ganze noch optimieren bzw. diskutieren. Wer hat Kommentare?--Schnirch 20:49, 25. Apr. 2013 (CEST)
- Wer traut sich einen Verbesserungsvorschlag zu machen?--Tutorin Anne 23:05, 2. Mai 2013 (CEST)
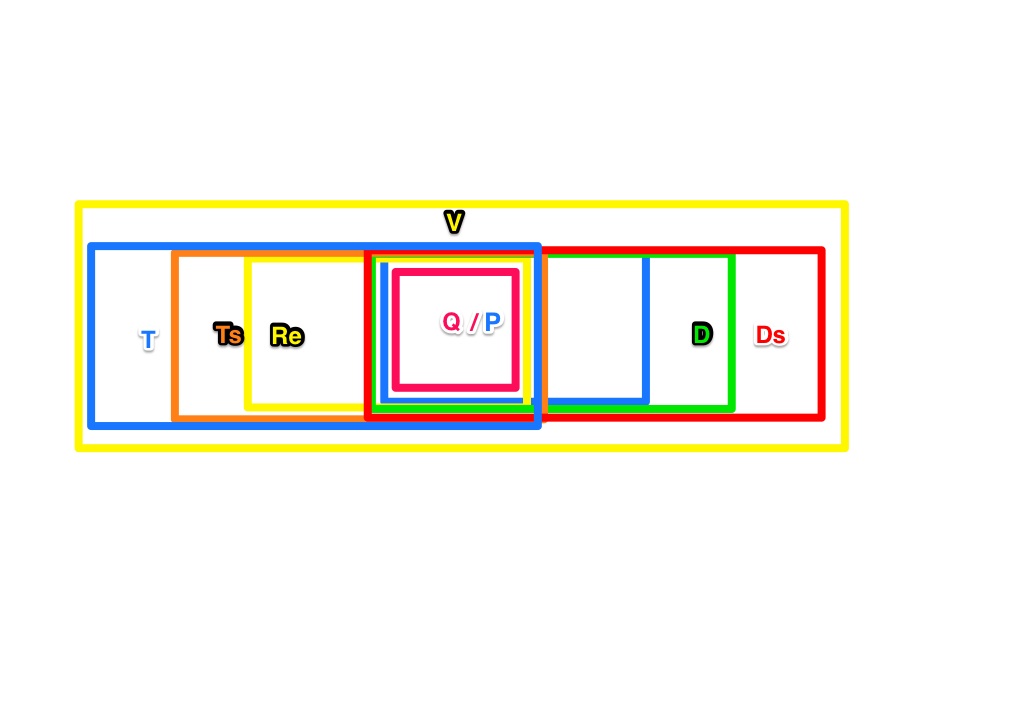
Das allg. Trapez muss dass Quadrat, Rechteck, gl. Trapez und das Parallelogramm beinhalten. Das sch. Drachenviereck muss dass Quadrat, die Raute, das gl. Drachenviereck und das Parallelogramm beinhalten. --Nolessonlearned 11:13, 3. Mai 2013 (CEST)
--Nolessonlearned 12:37, 3. Mai 2013 (CEST)
- Danke für deinen Beitrag, Nolessonlearned.
Der geschriebene Test stimmt. Das Quadrat ist eine Untermenge des allgemeinen Trapez. Damit muss der Kasten Quadrat des Venn-Diagramms auch komplett im all. Trapez-Kasten enthalten sein. Auf deinem Venn-Diagramm scheint es so, dass es auch Quadrate gibt, die keine allg. Trapeze sind. Das gilt genauso für die anderen Untergruppen. Somit ist das Venn-Diagramm, wie auch das obere, noch nicht korrekt.--Tutorin Anne 16:06, 5. Mai 2013 (CEST)
Hier nun die verbesserte Version:--Nolessonlearned 06:45, 6. Mai 2013 (CEST)
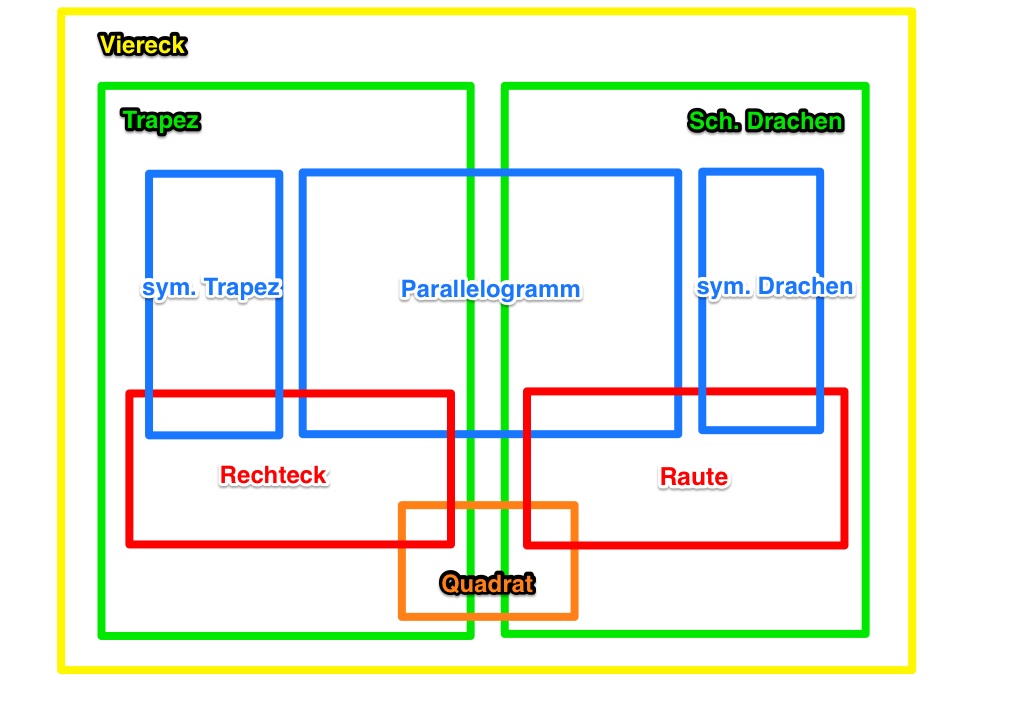
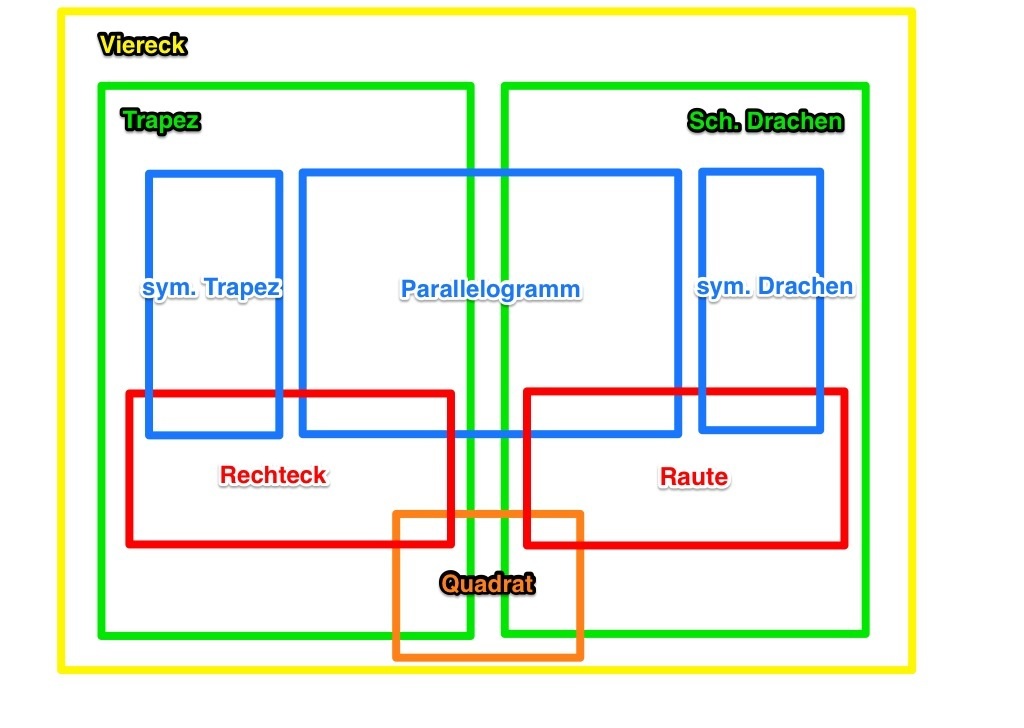
- Es gibt immer noch einen Teil des Quadrat-Kastens, der nicht im Trapez enthalten ist. (z.B. der Teil, der im schiefen Drachen enthalten ist. Das ist falsch.
Ein Venn-Diagramm mit Trapez, schiefem Drachen und Quadrat muss z.B. so aussehen:
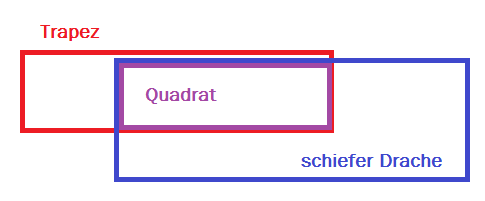--Tutorin Anne 12:56, 6. Mai 2013 (CEST)
- Habe Probleme dir zu folgen. Wie soll ich denn auf deine Weise eine Schnittmenge zwischen dem Quadrat und dem Rechteck hinbekommen, ohne dabei den schiefen Drachen Minden Rechteck zu schneiden? Das Rechteck ist ja keine Teilmenge des sch. Drachen. --Nolessonlearned 12:09, 7. Mai 2013 (CEST)
- Das Rechteck ist eben nur dann im Schiefen Drachen enthalten, wenn es ein Quadrat ist. Genau so muss es dann auch gezeichnet werden. Manchmal liegen mehrere Seiten "Linien" der Kästen übereinander.--Tutorin Anne 19:12, 8. Mai 2013 (CEST)
- Das Rechteck ist eben nur dann im Schiefen Drachen enthalten, wenn es ein Quadrat ist. Genau so muss es dann auch gezeichnet werden. Manchmal liegen mehrere Seiten "Linien" der Kästen übereinander.--Tutorin Anne 19:12, 8. Mai 2013 (CEST)
- So, mal ein anderer Ansatz.--Nolessonlearned 21:33, 8. Mai 2013 (CEST)
- Toll - das sieht schon viel besser aus! Allerdings frage ich mich, was für Parallelogramme das sind, die da oben "rausragen". Wie sehen Parallelogramm aus, die keine Trapeze sind?--Tutorin Anne 21:45, 11. Mai 2013 (CEST)
- Toll - das sieht schon viel besser aus! Allerdings frage ich mich, was für Parallelogramme das sind, die da oben "rausragen". Wie sehen Parallelogramm aus, die keine Trapeze sind?--Tutorin Anne 21:45, 11. Mai 2013 (CEST)
- Mh, das mit dem Parallelogramm stimmt noch nicht ganz. --Tutorin Anne 21:31, 13. Mai 2013 (CEST)
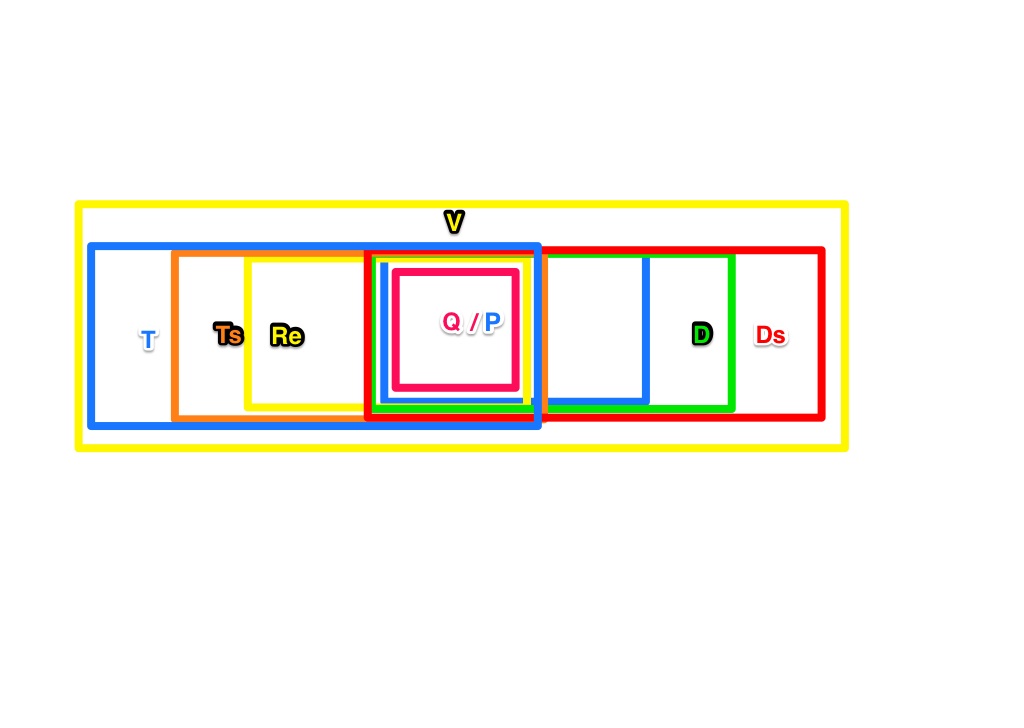--Nolessonlearned 09:08, 14. Mai 2013 (CEST)
- Wo ist die Raute? Ist das Rechteck kein Parallelogramm?--Tutorin Anne 14:35, 15. Mai 2013 (CEST)
- Ups. Frage mich auch wo die Raute geblieben ist. Das Parallelogramm ist auch ein Rechteck.--Nolessonlearned 17:08, 15. Mai 2013 (CEST)
- Ups. Frage mich auch wo die Raute geblieben ist. Das Parallelogramm ist auch ein Rechteck.--Nolessonlearned 17:08, 15. Mai 2013 (CEST)
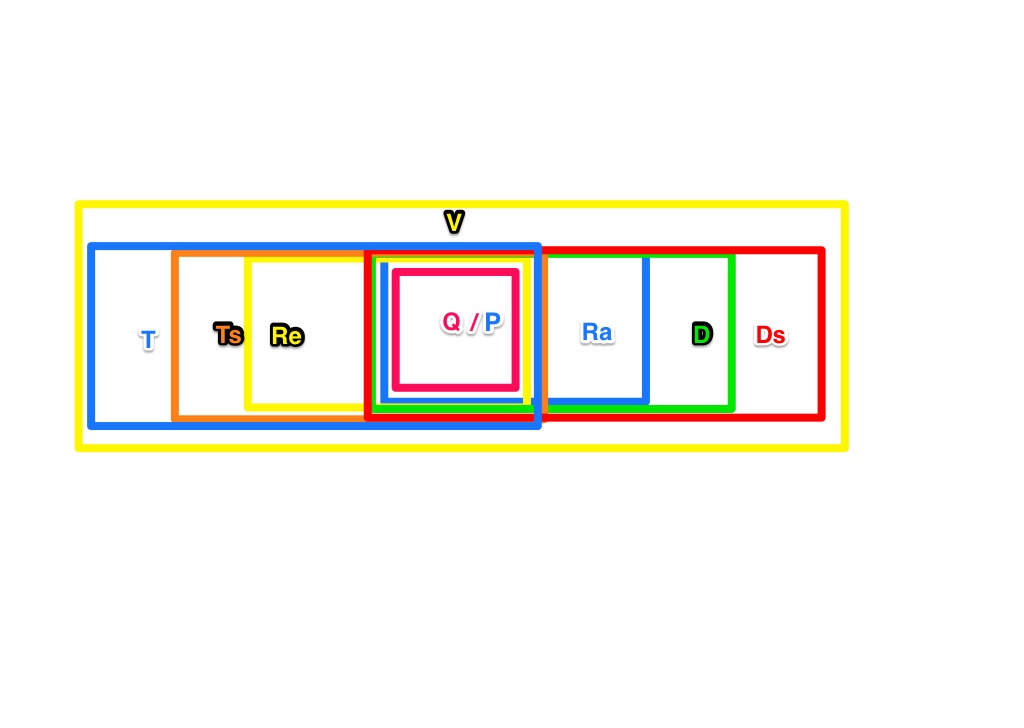--Nolessonlearned 17:08, 15. Mai 2013 (CEST)
- Das mit dem Parallelogramm stimmt noch nicht. Jedes Rechteck ist ein Parallelogramm (das sieht man nicht!). Zudem ist das korrekte Venn-Diagramm nicht rein linear (also ich meine durch Kästen nach rechts und links lösbar.) Tipp: Fang nochmal neu an und zwar mit dem Quadrat und ergänze dann die Oberbegriffe nacheinander. Überprüfe jede Teilmengenbeziehung und jedes Schnittmengenverhältnis.--Tutorin Anne 09:54, 23. Mai 2013 (CEST)
