Lösung von Zusatzaufgabe 3.1P (WS 13 14)

Geben Sie eine exakte Realdefinition des Begriffs Winkelhalbierende an (orientieren Sie sich gegebenenfalls an Schulbuchdefinitionen). Notieren Sie, welche anderen Begriffe Sie dazu verwenden.

Die Winkelhalbierende eines Winkels ist jene Halbgerade, welche durch den Scheitelpunkt des Winkels läuft und das Winkelgeld in zwei kongruente Winkel/Teile teilt. franziw

Franziw, deine Definition ist schon ganz gut. Du nennst richtig, dass es eine Halbgerade ist und der Winkel in zwei kongruente Winkel geteilt wird. Was meinst du eigentlich mit Winkelgeld?
Allerdings ist die Definition noch nicht exakt genug. Ich würde nach deiner Definition auch die rote und grüne Linien auf der Skizze (erstellt mit Paint - ganz einfach!) als Winkelhalbierenden verstehen.
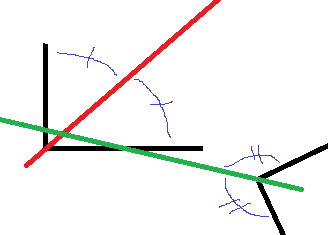--Tutorin Anne 18:51, 18. Nov. 2013 (CET)

Die Winkelhalbierende eines Winkels ist ein Strahl, der im Scheitelpunkt des Winkels beginnt und den Winkel in zwei kongruente Winkel teilt. --Der Kuckuck (Diskussion) 21:38, 9. Dez. 2013 (CET)

• Das ist schon eine gute Definition. Noch besser wäre es, wenn man darauf eingeht, dass die Winkelhalbierende im Inneren des Winkel liegt, denn so könnte auch ein Strahl gemeint sein, der wie die grüne Linie liegt, aber im Scheitel beginnt.--Tutorin Anne (Diskussion) 09:21, 12. Dez. 2013 (CET)