Lösung von Zusatzaufgabe 8.2P (WS 12 13)

Die nachfolgende GeoGebra-Applikation zeigt einen Billardtisch mit zwei Kugeln in der Draufsicht. Kugel A soll durch einen zentralen Stoß die Kugel B nun über drei Banden treffen. Konstruieren und Begründen Sie Ihre Konstruktion.

Wie kann ich hier ein Bild hochladen??--Hakunamatata 13:10, 9. Jan. 2013 (CET)

• Am linken Rand unter Werkzeuge - Datei hochladen, steht die Anleitung. Oder auf diesen Link klicken: http://wikis.zum.de/geowiki/Spezial:Hochladen --Tutorin Anne 07:54, 10. Jan. 2013 (CET)

Viele Danke, Anne. http://wikis.zum.de/geowiki/images/7/7e/2013-01-09_13.05.03.jpg --Hakunamatata 12:22, 11. Jan. 2013 (CET)

• Sehr schöne und richtige Konstruktion.
  
• Und wer übernimmt die Begründung?--Tutorin Anne 21:53, 13. Jan. 2013 (CET)

1. $S_g(\overline{AE})$ = $\overline{A'E}$
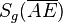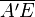
2. $\left| A'E \right|$ + $\left| ED \right|$ = $\left| A'D \right|$
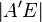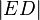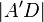
3. $S_h(\overline{A'D})$ = $\overline{A''D}$
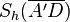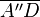
4. $S_k(\overline{BC})$ = $\overline{B'C}$
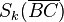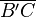
5. $\overline{A''B'}$ = $\overline{A''D}$ + $\overline{DC}$ + $\overline{CB'}$

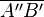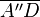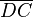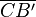
Ich glaube bei 5. müssen jeweils noch die Betragsstriche hinzugefügt werden. --TobiWan 15:08, 14. Jan. 2013 (CET)

Ich glaube im Grunde ist der Ansatz nicht verkehrt, bei der Billiardtischaufgabe geht es aber denke ich Primär um Feststellung " einfallswinkel = Außfallswinkel" hier kommt es uns ja nicht auf die kürzeste Strecke an, wie bei der "Feuerwehraufgabe"--Hakunamatata 22:01, 16. Jan. 2013 (CET)

• Aus mathematischer Sicht ist die gesuchte Strecke, die kürzeste Strecke, da die Geradenspiegelung so definiert ist. Daher ist die Begründung über die kürzeste Strecke ebenfalls richtig.--Tutorin Anne 15:56, 17. Jan. 2013 (CET)
• Aus physikalischer Sicht, muss der Einfallswinkel das gleiche Maß wie der Ausfallswinkel haben. Somit ist diesee Begründung ebenfalls richtig. (siehe das darunter eingestellte Bild von TobiWan)--Tutorin Anne 15:56, 17. Jan. 2013 (CET)

So könnte man das Begründen:
http://wikis.zum.de/geowiki/images/b/b6/Zusatzaufgabe8.2p.ws11.12.jpg
--TobiWan 00:23, 17. Jan. 2013 (CET)
Sehr gut, TobiWan und Hakunamatata!--Tutorin Anne 15:56, 17. Jan. 2013 (CET)