Lösung von Aufgabe 3.5 (WS 11/12)

Der Begriff Mittelsenkrechte sei folgendermaßen definiert:
Die Mittelsenkrechte einer Strecke $\overline{AB}$ ist die Gerade g, die durch den Mittelpunkt von $\overline{AB}$ verläuft und zu dieser Strecke $\overline{AB}$ senkrecht steht.
Beweisen Sie folgenden Satz:
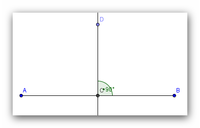
Die Mittelsenkrechte m einer beliebigen Strecke $\overline{AB}$ ist die Menge aller Punkte P, die von A und B denselben Abstand haben:
(Beachten Sie, dass auch dieser Beweis wieder aus zwei Teilen besteht analog zur Aufgabe 3.4).

Voraussetzungen:

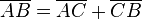$\overline{AB} = \overline{AC} + \overline{CB}$ der Mittelpunkt der Strecke AB ist der Punkt C

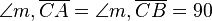$\angle m, \overline{CA} = \angle m, \overline{CB} = 90$° m ist die Mittelsenkrechte; D ein exemplarisch verwendeter Punkt auf m

Behauptung:

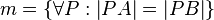$m = \left\{ {\forall P:\left| PA \right| = \left| PB \right| } \right\}$ Alle Punke mit der Eigenschaft, dass der Abstand zu A und B gleich ist, bilden die Mittelsenkrechte

Beweis:

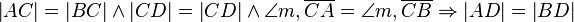$\left| AC \right| = \left| BC \right| \wedge \left| CD \right| = \left| CD \right| \wedge \angle m, \overline{CA} = \angle m, \overline{CB}\Rightarrow \left| AD \right| = \left| BD \right|$ SsW Die dreiecke sind konguent, somit muss auch der Abstand identisch sein. Somit liegt D auf m

• So habe ich das auch gelöst, nur dass ich dabei mit SWS begründet habe. Außerdem könnte man das letzte "somit liegt D auf m" weglassen, da wir ja davon ausgegangen sind, dass D auf m liegt und nur beweisen müssen, dass jeder Punkt Element von m zu den Endpunkten der Strecke AB denselben Abstand hat. :)--Miriam 17:00, 1. Nov. 2011 (CET)
  • Ja ist mit SWS genauso möglich, ist sogar noch einfacher, ich denke wir müssen in zwei Schritten beweisen, es handelt sich hier um Äquvalenz, deswegen in beide Richtungen, erst dass ein Punkt mit diesen Abständen auf m liegt und dann, dass es auch keinen Punkt mit diesen Abständen gibt, welcher nicht auf m liegt. --RicRic
    • @Miriam Hi Miriam, wenn du die hübsche Saarländerin bist und mit mir im Tutorium, denk daran, dass du mir noch das eine Dokument schicken wolltest. Danke --RicRic
  • bei deinem Schritt RicRic ist es der Satz SWS. Und: Die Äquivalenz beweist du durch die zwei Teile des Beweises, hier nicht innerhalb eines Beweises bzw. Schrittes.--Tutorin Anne 10:39, 3. Nov. 2011 (CET)

Annahme:

$\exists P\not\in m \wedge \left| AP \right|= \left| BP \right|$

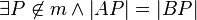
Beweis Teil 2:

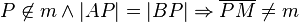$P\not\in m \wedge \left| AP \right|= \left| BP \right| \Rightarrow \overline{PM} \neq m$ Es muss dan also eine Gerade geben welche die Punke P und M schneidet jedoch nicht die Mittelsenkrechte ist, sonst wäre ja P Element m

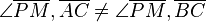$\angle \overline{PM},\overline{AC} \neq \angle \overline{PM},\overline{BC}$ Da es dich nicht um die Mittelsenkrechte handelt, müssen die Winkel auch unterschiedlich sein.

SSS - Wenn die drei Seiten des Dreiecks konguent sind müssen die Winkel es auch sein. Also muss P Element m sein. --RicRic

• Allgemein zu diesem Beweis: Es ist besser, wenn du klar aufzeigst, welcher Teil des Beweises jetzt vorliegt. Nenne dazu nochmal die Voraussetzung (die sich teils verändert) und die Behauptung (in Worten oder mit Formeln). Falls du indirekt beweist, anschließend die Annahme.
  
• Ein indirekter Beweis macht dann Sinn, wenn du die Annahme direkt verwendest. Wenn sie aber nur am Ende für den Widerspruch nötig ist, kannst du auch direkt vorgehen.
  

Andere Vorschläge?--Tutorin Anne 10:39, 3. Nov. 2011 (CET)