NAF zweier zentrischer Streckungen (EM 2012 :-))

Vorbereitungsspiel

Weil ja schließlich morgen EM ist, bleibt mir fast nichts anderes übrig, als das folgende Kapitel mit einem Fußballbeispiel einzuführen: Da Jogis Jungs am Samstag ja gegen Portugal spielen, wird es sich darauf hinauslaufen.

Ausgangssituation

Wir gehen von folgendem Radiomittschnitt aus (nicht jeder hat einen Fernseher :-)):
"Jetzt wird es spannend, der Ball liegt knapp vor dem Kasten der Portugiesen. Eduardo bewegt sich aber im Moment noch gar nicht, Gomez und Klose lauern. Wie wir Gomez kennen, ist er wieder einmal meilenweit vom Ball entfernt, ersten Schätzungen zufolge ist er genau zweimal soweit vom Ball entfernt, wie von Miro Klose. Das ist jetzt interessant - der Rasen scheint zu brennen, das Spiel lebt von der Spannung. Man kann fast von Rasenschach sprechen - die Luft knistert und auch dem Spielern scheint vor lauter Spannung die Bewegung abhanden gekommen zu sein. Erstaunlicherweise ist auch Ricardo, der portugiesische Abwehrspieler von seinem Torwart genau zweimal soweit entfernt, wie er selbst vom Ball, was in diesem speziellen Fall nichts anderes heißt, als dass sie beide gleich weit vom Ball entfernt sind. Es bewegt sich gar nichts. Nichts, es scheint fast so als hätten wir ein Standbild. Oh, zumindest einer bewegt sich: Ronaldo sitzt auf dem Rasen und schneidet sich die Fußnägel. Er ist im übrigen von seinem Torwart viermal so weit entfernt, wie von Klose, also selbst wenn er seine Fußnägel geschnitten hätte, wäre Klose viel schneller am Ball als Ronaldo. Aber wir brauchen uns diesbezüglich keine Gedanken machen, da sich Ronaldo nur auf einer Linie nach vorne bewegen kann - auf der Linie nämlich, auf der auch Klose und Ricardo stehen.
Für all diejenigen, denen das Spiel zu langweilig ist, können sich ja mal mit zentrischer Streckung befassen. Welcher Zusammenhang besteht denn zwischen Gomez, Ronaldo und Ricardo Costa?"

Ok, ich geb' zu - ist ein bisschen an den Haaren herbeigezogen (bzw. an den Fußnägeln :-)). Nichts desto trotz hat das öffentlich rechtliche Fernsehen einen Bildungsauftrag und vielleicht kommt sowas ja irgendwann mal vor :-). Wenn nicht, hier wirds trotzdem kurz bearbeitet:


bist du auf droge?  :-)
--Studentin 12:45, 8. Jun. 2012 (CEST)

ne, aber ich wär echt mal gern fußballkommentator :D --Flo60 15:04, 8. Jun. 2012 (CEST)

Flo scheint mir ein Repräsentant einer so relevanten wie lästigen Äquivalenzklasse auf der Menge aller Menschen mit deutscher Staatsbürgerschaft zu sein. Fußballexperten aller Schichten, vereinigt euch! Dr.plag.Schavan (Diskussion) 15:14, 31. Jul. 2014 (CEST)

Was soll nun eigentlich gezeigt werden?

Schlussendlich geht es natürlich um die NAF zweier zentrischer Streckungen. Hier die Skizze nochmal - ein wenig verändert:

Wie nun ersichtlich ist ist unsere Abbildung die folgende: NAF 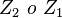$Z_2 \ o \ Z_1$.

Die NAF ist erneut zentrische Streckung (wir besser ersichtlich weiter unten aufgrund der Parallelität und der veränderten Größe der Dreiecke - ist mit einzelnen Punkten schwierig darzustellen).
Es bleibt herauszufinden, wo nun unser fehlender Spieler ist - nämlich Ronaldo. Es muss wohl so sein, dass er auf 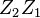$Z_2Z_1$ zu finden ist.

Begründung

R ist muss nach der NAF wieder auf sich selbst abgebildet werden (Streckzentrum ist Fixpunkt bei ZS)

Wenn ein Punkt R von $Z_1$ aus gestreckt wird, dann ist er auf $Z_1R$. 

Da $ZS_Z1,k(R)$ nun allerdings wieder auf R abgebildet werden muss, und R = R auf R'B liegen muss, 
liegt liegt R und R' auf $Z_1Z_2$.

In der 'Skizze unten' kann eine Schar von Geraden angezeigt werden, das kann gerade beschriebenes verdeutlichen.

In welchem Verhältnis stehen nun die Punkte Z1, Z2 und R?

Hier wieder eine Skizze:

Berechnung

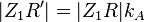
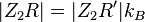
Nun gilt folgendes: $|Z_1R'| = |Z_1R|k_A$ $|Z_2R| = |Z_2R'|k_B$

Ferner gilt: 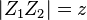$|Z_1Z_2| = z$ und $|Z_1R| = r$

$r = z - (Z_2-R')*k_B$
$r = z - (z-k_A*r)*k_B$
$r = z - z*k_B + k_A*r*k_B)$
$r = z(1-k_B) + k_A*k_B*r$
$r - k_A*k_B*r = z(1-k_B)$
$r(1 - k_A*k_B) = z(1-k_B)$
$r = z \frac{(1-k_B)} {(1 - k_A*k_B)}$

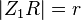
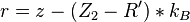
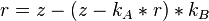
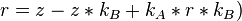
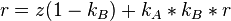
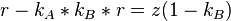
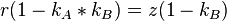
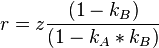
Schlusswort: Heftige Geometrie! :-) Da schau ich mir das Spiel doch lieber im Fernsehen an! :-) --Flo60 18:33, 7. Jun. 2012 (CEST)

Kontrolle - Didaktisch sinnvoll, nicht nur in Grund- und Hauptschule :-) - auch wenns kein Beweis ist

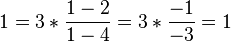$1 =3* \frac{1-2} {1-4} = 3*\frac{-1} {-3} = 1$ - tada! --Flo60 18:40, 7. Jun. 2012 (CEST)

Zurück zur Übersichtsseite

Das WIKI für die Veranstaltung Elementargeometrie