Probeklausur (WS 11/12)

Aufgabe 1

Definieren Sie den Begriff Mittelpunkt einer Strecke $\overline{AB}$.

Lösung von Aufg. 1 (WS_11/12)

Aufgabe 2

Ergänzen Sie die nachfolgende Definition des Begriffs Halbkreis (Definition Kreis sei vorausgesetzt).
Definition (Halbkreis): Es sei k ein Kreis mit dem Mittelpunkt M. …

Lösung von Aufg. 2 (WS_11/12)

Aufgabe 3

Ergänzen Sie die nachfolgende Definition des Begriffs Inneres einer Kugel (Definition Kugel sei vorausgesetzt).
Definition (Inneres einer Kugel): Es sei k eine Kugel mit dem Mittelpunkt M und dem Radius r.
Inneres einer Kugel:= 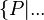$\{P|...$

Lösung von Aufg. 3 (WS_11/12)

Aufgabe 4

Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?

Lösung von Aufg. 4 (WS_11/12)

Aufgabe 5

Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz Das Innere eines Winkels ist konvex.)

Lösung von Aufg. 5 (WS_11/12)

Aufgabe 6

Gegeben sei die Halbebene 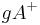$\ gA^{+}$ und ein Punkt $B\in \ gA^{+}$.
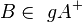Beweisen Sie:
$\forall X: X\in \ gA^{+}\Rightarrow X\in \ gB^{+}$

Lösung von Aufg. 6 (WS_11/12)

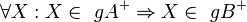
Aufgabe 7

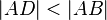Gegeben sei ein Punkt D auf einem Strahl $\ AB^{+}$ , mit $\left| AD \right| <\left| AB \right|$. Zeigen Sie, dass dann gilt: Zw(A,D,B).

Lösung von Aufg. 7 (WS_11/12)