Sehnenvierecke und der Satz über die gegenüberliegenden Winkel im Sehnenviereck WS 11/12

Begriff des Sehnenvierecks

Definition XVIII.1: (Kreissehne)

Das können Sie selbst:

Eine Kreissehne ist eine Strecke, deren Endpunkte Elemente des Kreises sind.--Schambes 13:52, 21. Jan. 2012 (CET)

Definition XVIII.2: (die Durchmesser eines Kreises)

Das können Sie selbst. Hinweis: Jeder Kreis hat unendlich viele Durchmesser.

Die Durchmesser eines Kreises sind die Sehnen des Kreises, bei denen der Mittelpunkt des Kreises Element der Sehnen ist.--Schambes 13:54, 21. Jan. 2012 (CET)

Definition XVIII.3: (Radien eines Kreises)

Das können Sie selbst. Hinweis: Jeder Kreis hat unendlich viele Radien.

Die Radien eines Kreises sind die Strecken, deren einer Endpunkt der Mittelpunkt ist und der andere Endpunkt Element des Kreises ist.--Schambes 13:57, 21. Jan. 2012 (CET)

Definition XVIII.4: (Sehnenviereck)

Ein Viereck, dessen Seiten Sehnen ein und desselben Kreises $k$ sind, heißt Sehnenviereck.

Der Satz über die gegenüberliegenden Winkel im Sehnenviereck

Die Satzfindung

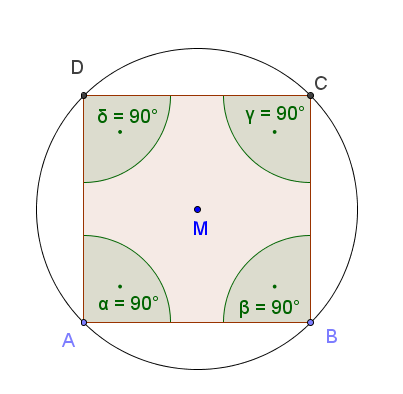
sehr speziell: Quadrate

Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.

weniger speziell, aber immer noch ziemlich speziell: Rechtecke

Jedes Rechteck ist ein Sehnenviereck.

noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze

Jedes gleichschenklige Trapez ist ein Sehnenviereck.

allgemeines Sehnenviereck

Ausgangslage: $\overline{ABCD}$ ist ein gleichschenkliges Trapez.

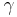Arbeitsauftrag: Bewegen Sie den Punkt $C$ auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von $\gamma$? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?

Der Satz über die gegenüberliegenden Winkel im Sehnenviereck