Aufgabe 2.1
Unter einer Untergruppe einer Gruppe ![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) versteht man eine Teilmenge versteht man eine Teilmenge 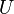 von von  , die bezüglich , die bezüglich  sie eine Gruppe ist. Erstellen sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates und stellen Sie Beziehungen zum Haus der Vierecke her. sie eine Gruppe ist. Erstellen sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates und stellen Sie Beziehungen zum Haus der Vierecke her.
Aufgabe 2.2
Stellen Sie die Gruppen des Untergruppengraphen aus Aufgabe 2.1 in der Form von Matrizengruppen dar.
Aufgabe 2.3
Beweisen Sie: In jeder Gruppe ist für beliebige ![[G,\otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) sind die Gleichungen sind die Gleichungen 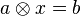 und und 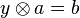 immer eindeutig lösbar für beliebige immer eindeutig lösbar für beliebige 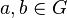 . .
Aufgabe 2.4.
Beweisen Sie: In jeder Gruppe ![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) gilt für beliebige gilt für beliebige 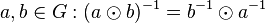 . .
Aufgabe 2.5
Es sei ![[G, \oplus]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) eine Gruppe. Beweisen Sie: In der Gruppentafel von eine Gruppe. Beweisen Sie: In der Gruppentafel von ![[G, \oplus ]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) tritt jedes Element aus tritt jedes Element aus  in jeder Zeile und in jeder Spalte genau einmal auf. in jeder Zeile und in jeder Spalte genau einmal auf.
Aufgabe 2.6
Unter der Ordnung 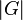 einer Gruppe einer Gruppe ![[G,\cdot]](/images/math/8/9/3/8932b57f872fc473578a144826c5f44c.png) versteht man die Anzahl der Elemente von versteht man die Anzahl der Elemente von  .
Untersuchen Sie die Untergruppengraphen aus Aufgabe 2.1 hinsichtlich der auftretenden Gruppenordnungen in diesem Graphen. Was stellen Sie fest? .
Untersuchen Sie die Untergruppengraphen aus Aufgabe 2.1 hinsichtlich der auftretenden Gruppenordnungen in diesem Graphen. Was stellen Sie fest?
Aufgabe 2.7
Unter der Ordnung 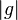 eines Elementes eines Elementes  einer Gruppe einer Gruppe ![[G,+]](/images/math/e/c/8/ec8a9c4caaa293defc4743bd3e86ee6f.png) versteht man die kleinste Zahl versteht man die kleinste Zahl 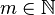 für die gilt für die gilt 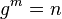 , wobei unter , wobei unter  das neutrale Element der Gruppe das neutrale Element der Gruppe ![[G,+]](/images/math/e/c/8/ec8a9c4caaa293defc4743bd3e86ee6f.png) zu verstehen ist. Bestimmen Sie alle Elementordnungen in folgenden Gruppen zu verstehen ist. Bestimmen Sie alle Elementordnungen in folgenden Gruppen
- Restklassen modulo
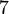 bezüglich der Restklassenaddition, bezüglich der Restklassenaddition,
- Restklassen modulo
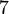 bezüglich der Restklassenmultiplikation. bezüglich der Restklassenmultiplikation.
Aufgabe 2.8
Es sei ![[G,*]](/images/math/8/b/a/8ba79871f2859f4de44b792bf88add3a.png) eine Gruppe in deren Gruppentafel in der Hauptdiagonalen an jeder Position das Einselement eine Gruppe in deren Gruppentafel in der Hauptdiagonalen an jeder Position das Einselement  der Gruppe der Gruppe ![[G,*]](/images/math/8/b/a/8ba79871f2859f4de44b792bf88add3a.png) auftritt. Was wissen Sie über die Ordnungen aller Elemente von auftritt. Was wissen Sie über die Ordnungen aller Elemente von ![[G,*]](/images/math/8/b/a/8ba79871f2859f4de44b792bf88add3a.png) ? ?
Aufgabe 2.9
Eine zyklische Gruppe ist eine Gruppe, in der es ein Element gibt, dessen Ordnung gleich der Gruppenordnung ist. Beweisen Sie: zyklische Gruppen sind immer kommutativ.
Aufgabe 2.10
Beweisen Sie:
- Es gibt genau eine Typ von Gruppen der Ordnung 3.
- Es gibt genau zwei Typen von Gruppen der Ordnung 4.
| ![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) versteht man eine Teilmenge
versteht man eine Teilmenge 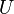 von
von  , die bezüglich
, die bezüglich  sie eine Gruppe ist. Erstellen sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates und stellen Sie Beziehungen zum Haus der Vierecke her.
sie eine Gruppe ist. Erstellen sie einen Untergruppengraphen der Gruppe der Deckabbildungen des Quadrates und stellen Sie Beziehungen zum Haus der Vierecke her.
![[G,\otimes]](/images/math/0/1/3/01322720752789c5d9651172aee2d990.png) sind die Gleichungen
sind die Gleichungen 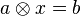 und
und 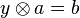 immer eindeutig lösbar für beliebige
immer eindeutig lösbar für beliebige 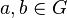 .
.
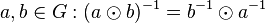 .
.
![[G, \oplus]](/images/math/7/6/a/76a5019aba25ee8b54b799a29a626d33.png) eine Gruppe. Beweisen Sie: In der Gruppentafel von
eine Gruppe. Beweisen Sie: In der Gruppentafel von 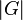 einer Gruppe
einer Gruppe ![[G,\cdot]](/images/math/8/9/3/8932b57f872fc473578a144826c5f44c.png) versteht man die Anzahl der Elemente von
versteht man die Anzahl der Elemente von 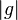 eines Elementes
eines Elementes  einer Gruppe
einer Gruppe ![[G,+]](/images/math/e/c/8/ec8a9c4caaa293defc4743bd3e86ee6f.png) versteht man die kleinste Zahl
versteht man die kleinste Zahl 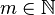 für die gilt
für die gilt 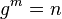 , wobei unter
, wobei unter  das neutrale Element der Gruppe
das neutrale Element der Gruppe  bezüglich der Restklassenaddition,
bezüglich der Restklassenaddition,
![[G,*]](/images/math/8/b/a/8ba79871f2859f4de44b792bf88add3a.png) eine Gruppe in deren Gruppentafel in der Hauptdiagonalen an jeder Position das Einselement
eine Gruppe in deren Gruppentafel in der Hauptdiagonalen an jeder Position das Einselement  der Gruppe
der Gruppe 
