Serie 06 12 13

Aufgabe 6.1

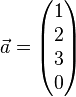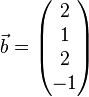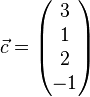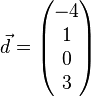Zeigen Sie, dass die Vektoren $\overrightarrow{a}=\left(\begin{array}{c}1\\ 2\\ 3\\ 0\end{array}\right)$, $\overrightarrow{b}=\left(\begin{array}{c}2\\ 1\\ 2\\ -1\end{array}\right)$, $\overrightarrow{c}=\left(\begin{array}{c}3\\ 1\\ 2\\ -1\end{array}\right)$ und $\overrightarrow{d}=\left(\begin{array}{c}-4\\ 1\\ 0\\ 3\end{array}\right)$ linear abhängig sind und überprüfen Sie, welche(r) der Vektoren sich als Linearkombination der jeweils anderen drei Vekotren darstellen lässt/lassen.

Aufgabe 6.2

Sei V ein reeler Vektorraum und 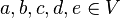$a,b,c,d,e\in V$. Zeigen Sie, dass die folgenden Vektoren linear abgängig sind:
$v_1=a+b+c$, $v_2=2a+2b+2c-d$, $v_3=a-b-e$, $v_4=5a+6b-c+d+e$, $v_5=a-c+3e$, $v_6=a+b+d+e$

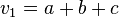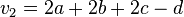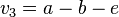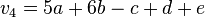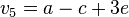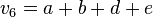
Aufgabe 6.3

Geben Sie für folgende Vektorräume eine Basis an:
a) 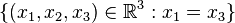$\{(x_1,x_2,x_3)\in {\mathb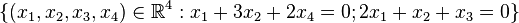b{ℝ}}^3:x_1=x_3\}$
b)$\{(x_1,x_2,x_3,x_4)\in {\mathbb{ℝ}}^4:x_1+3x_2+2x_4=0;2x_1+x_2+x_3=0\}$

Aufgabe 6.4

Bestimmen Sie die Koordinaten des Vekotrs 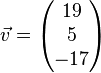$\overrightarrow{v}=\left(\begin{array}{c}19\\ 5\\ -17\end{array}\right)$ bezüglich der Basis $B=\{\left(\begin{array}{c}1\\ 2\\ 3\end{array}\right);\left(\begin{array}{c}-4\\ -5\\ -6\end{array}\right);\left(\begin{array}{c}7\\ 8\\ 7\end{array}\right)\}$