Serie 07 12 13

Aufgabe 7.1

Austauschlemma:
Sei 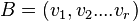$B=(v_1, v_2 .... v_r)$Basis und 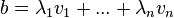$b=\lambda_1v_1+...+\lambda_nv_n$. Falls 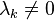$\lambda_k \neq 0$ ist (für ein 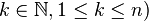$k \in \mathbb{N}, 1 \le k \le n)$, so ist auch die Menge 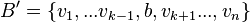$B'=\{v_1,... v_{k-1}, b, v_{k+1}..., v_n\}$ eine Basis von V.

Beweisen Sie das Lemma.

(Veranschaulichen Sie das Lemma mit einem konkreten Beispiel.)

Aufgabe 7.2

Bestimmen Sie eine Basis des von der Menge erzeugenten Vektorraum U=<X>.
$X=\{\begin{pmatrix} 0 \\ 1 \\0 \\-1 \end{pmatrix};\begin{pmatrix} 1 \\ 0 \\ 1\\-2 \end{pmatrix}; \begin{pmatrix} -1 \\ -2 \\ 0\\1 \end{pmatrix}; \begin{pmatrix} -1 \\ 0 \\ 1\\0 \end{pmatrix}; \begin{pmatrix} 1 \\ 0 \\ -1\\-1 \end{pmatrix}; \begin{pmatrix} 2 \\ 0 \\ -1\\0 \end{pmatrix}\}.$
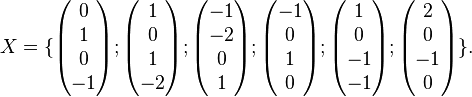
Gilt 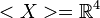$<X>=\mathbb{R}^4$?

Aufgabe 7.3

Konstruieren Sie eine Basis für den von $v_1 = (1,-2,0,1)\,,\;\, v_2 = (0,0,2,5)\,, \;\, v_3 = (-2,4,2,3)$

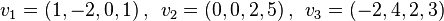
erzeugten Vektorraum und ergänzen Sie diese Basis zu einer Basis von 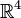${\mathbb R}^4$.

Aufgabe 7.4

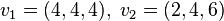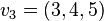a) Prüfen Sie, ob die Vektoren $v_1 = (4,4,4),\; v_2 = (2,4,6)$ und $v_3 = (3,4,5)$ ein Erzeugendensystem von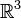${\mathbb R}^3$ bilden.
b) Untersuchen Sie, für welche 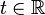$t \in {\mathbb R}$ die Vektoren 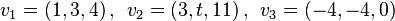$v_1 = (1,3,4)\,, \;\, v_2 = (3,t,11)\,, \;\, v_3 = (-4,-4,0)$ linear abhängig in 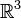${\mathbb R}^3$ sind.